11.1. ОБЩАЯ ХАРАКТЕРИСТИКА ЧАСТОТНОГО АНАЛИЗА ЦЕПЕЙ. СПЕКТРАЛЬНОЕ ПРЕДСТАВЛЕНИЕ ПЕРИОДИЧЕСКИХ СИГНАЛОВ

Простота анализа цепей, находящихся под действием синусоидальных сигналов, определяется тем, что зависимости от времени токов и напряжений во всех ветвях в этом случае имеют одинаковую форму и частоту и различаются лишь амплитудами и начальными фазами. Поэтому задача расчета цепи сводится к определению комплексных амплитуд (или действующих значений) искомых величин, которая решается чисто алгебраическими средствами.

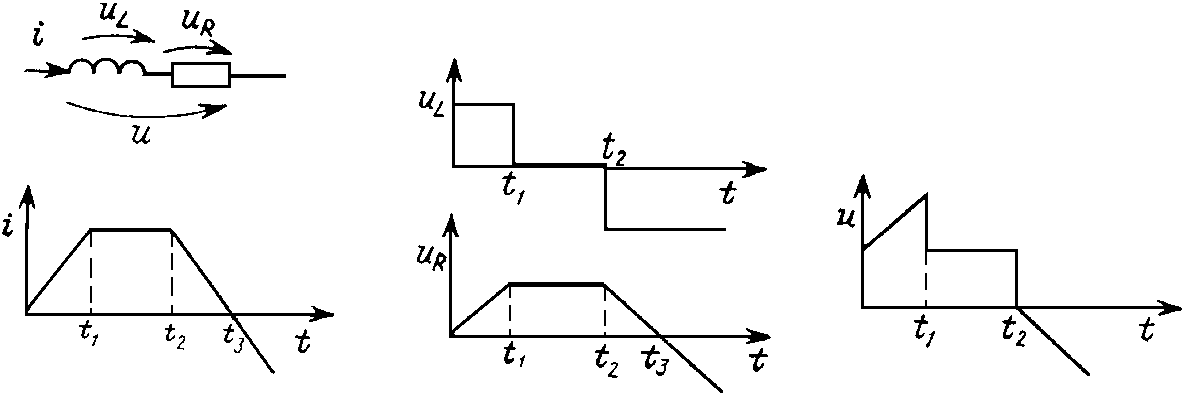
При действии несинусоидального сигнала в цепи, содержащей динамические элементы L и C, кривые токов и напряжений отдельных ветвей имеют различную форму. Так, для участка цепи с последовательным соединением R, L, по которым протекает ток i (рис. 11.1), будем иметь u = u_L + u_R = L di/dt + Ri, и кривые u_L, u_R и u различны. Это существенно усложняет задачу анализа цепей при несинусоидальных токах по сравнению с синусоидальным током.

Рис. 11.1

Один из возможных путей расчета — частотный (спектральный) метод основан на представлении действующих в цепи несинусоидальных сигналов в виде совокупности синусоидальных составляющих с различными частотами — спектра сигнала. Математической базой для спектрального представления сигналов являются аппарат рядов Фурье для периодических функций и интегралов Фурье — для непериодических. Анализ цепи под действием каждой отдельной синусоидальной составляющей производится с помощью комплексного метода. Для нахождения временнóй зависимости искомой величины используют принцип наложения.

Описанный подход и составляет частотный (спектральный) метод расчета цепи. Он имеет широкое распространение при анализе самых разнообразных физических процессов. Поскольку основная часть расчетов при этом выполняется в частотной области, то спектры сигналов и частотные свойства цепей обычно представляют больший интерес чем их описание во временной области. 

Сигнал, обладающий свойством периодичности f(t) = f(t + T) (рис. 11.2), удовлетворяющий условиям Дирихле, может быть представлен в виде ряда Фурье:

(11.1)

где

A₀ — постоянная составляющая; B_k, C_k — коэффициенты Фурье; w_k = 2pk/T — частоты отдельных синусоидальных составляющих (гармоник), кратные частоте основной (первой) гармоники w₁ = 2p/T, период которой совпадает с периодом исходного сигнала T.

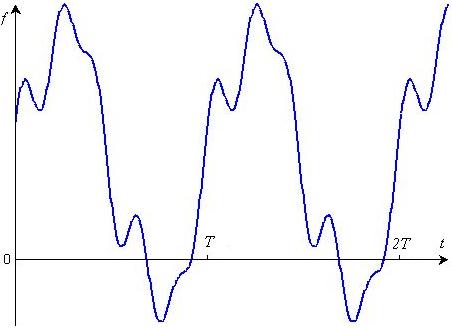
Рис. 11.2

Записанное представление f(t) определяет так называемую тригонометрическую форму ряда Фурье. Она может быть приведена к амплитудно-фазовой форме, наглядно выражающей представление периодического сигнала f(t) в виде суммы синусоидальных составляющих — гармоник с кратными частотами w_k, амплитудами A_k и начальными фазами y_k:

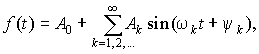(11.2)

где

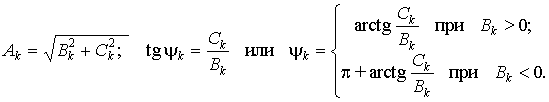
Наиболее компактной и удобной для расчетов формой записи является экспоненциальная (комплексная) форма ряда Фурье, для перехода к которой воспользуемся формулой Эйлера e^±jwt = cos wt ± j sin wt. Замена тригонометрических функций в ряде (11.1) на экспоненты и группировка экспонент с показателями jw_kt и – jw_kt приводит его к виду

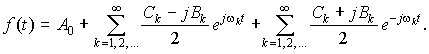
Используя выражения для коэффициентов тригонометрической формы C_k и B_k, запишем комплексные коэффициенты (jw_k) = (C_k – jB_k)/2 первой из полученных сумм

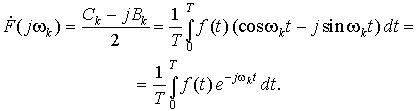
Вторую сумму можно привести к аналогичному виду, используя отрицательные индексы суммирования q = – k. Поскольку w_k = – w_q, C_k = C_q, а B_k = – B_q, то и эта сумма может быть записана в виде

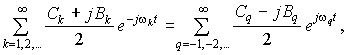
полностью совпадающем по виду с первой суммой, но с отрицательными значениями индекса. Очевидно, и член A₀ можно записать в таком же виде при k = 0. Поэтому экспоненциальный ряд Фурье можно представить в виде единой суммы, содержащей индексы суммирования от – до +, включая значение k = 0:

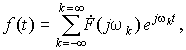(11.3)

где

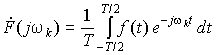(11.4)

— комплексные коэффициенты ряда. В последнем интеграле пределы интегрирования от 0 до T заменены симметричными пределами от – T/2 до + T/2, что не изменяет его значения. Именно такое представление является традиционным для комплексной формы ряда Фурье. Таким образом, эта форма требует вычисления лишь одного комплексного интеграла (11.4). 

Суммирование в (11.3) включает не имеющие реального смысла "отрицательные частоты" w_-k = -2kp/T — члены ряда с отрицательными индексами k. Подобная запись наиболее компактна по сравнению с другими формами и, как мы увидим в дальнейшем, является наиболее удобной для расчетов. 

Комплексные коэффициенты ряда Фурье = (C_k – jB_k)/2 позволяют непосредственно выразить амплитуды гармоник A_k = 2 и их начальные фазы y_k = arg + p/2. Поэтому комплексная амплитуда k-й гармоники . Для постоянной составляющей имеем A₀ = F(0). Отсюда следует также, что комплексные коэффициенты с положительными и отрицательными индексами являются комплексно сопряженными: .

Совокупность комплексных коэффициентов рассматриваемой функции образует ее спектр. Так как в спектре периодического сигнала (рис. 11.3, а) присутствуют только частоты, кратные частоте основной (первой) гармоники w_k = (2p/T)k = w₁k, то изображение такого спектра, на котором по оси абсцисс откладывают значения частоты, а по оси ординат — соответствующие им амплитуды, имеет дискретный характер (рис. 11.3, б). Поскольку зависимость амплитуд от частоты является четной функцией, то ее достаточно изобразить лишь для положительных значений частоты. Однако такой спектр не содержит полной информации о сигнале, которую необходимо либо дополнить частотной зависимостью начальных фаз y_k, либо привести распределение вещественной и мнимой частей .

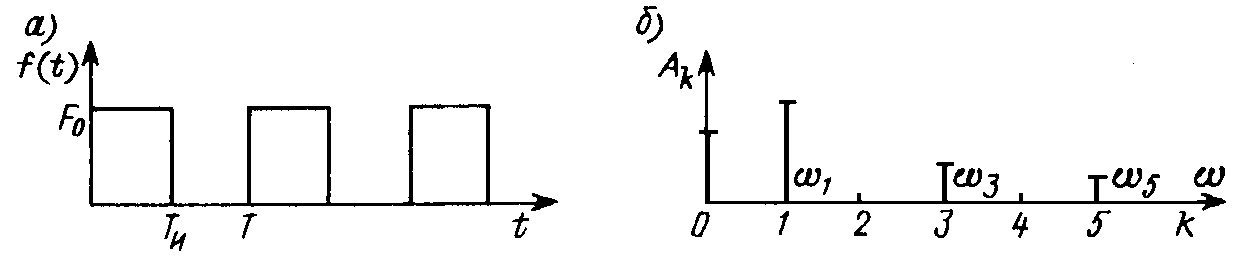
Рис. 11.3

Определим спектр периодической последовательности прямоугольных импульсов длительностью T_и с амплитудами F₀ (рис. 11.3, а). Поскольку выражение временнóй зависимости рассматриваемого сигнала на периоде имеет вид

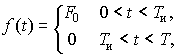
то для коэффициентов получим, используя интеграл (11.4) с пределами интегрирования (0, T)

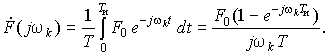
Используя формулу Эйлера, представим найденное выражение с учетом соотношения w_kT = 2pk в виде

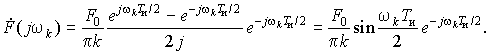
Отсюда следует, что амплитуда k-й гармоники равна

а ее начальная фаза

Постоянная составляющая анализируемого сигнала равна A₀ = F(0) = F₀T_и/T. Спектр амплитуд для T_и/T = 0,5 изображен на рис. 11.3, б. Кроме постоянной составляющей, он содержит лишь нечетные гармоники, первые из которых (k = 1, 3, 5) построены на рис. 11.3, а. Очевидно, что с ростом числа учитываемых гармоник их сумма приближается к исходной кривой f(t).

Сигналы, обладающие определенной симметрией, имеют более простые выражения коэффициентов Фурье. Так, если функция  f(t) является четной [ f(–t) =  f(t)], ее тригонометрическое представление содержит лишь косинусоиды (B_k = 0), а комплексные коэффициенты   — вещественные. Спектр нечетной функции [f(–t) = – f(t)], наоборот, содержит лишь синусоидальные составляющие (С_k = 0), и его коэффициенты являются чисто мнимыми.

Четные гармоники и постоянная составляющая отсутствуют в спектре нечетно-гармонических сигналов, у которых каждая полуволна повторяет предыдущую с переменой знака (рис. 11.4), описываемых соотношением f(t) = – f(t – T/2). Действительно, из выражения для их комплексных коэффициентов имеем:

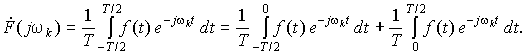
Рис. 11.4

Последний интеграл путем замены переменной t = t' + T/2 с учетом симметрии можно привести к виду

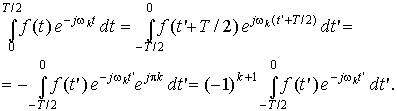
Поскольку только что полученный интеграл совпадает с интегралом первого слагаемого в выражении для коэффициента , приведем это выражение к окончательному виду

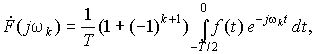
откуда и следует, что для четных значений k имеем F(jw_k) = 0.