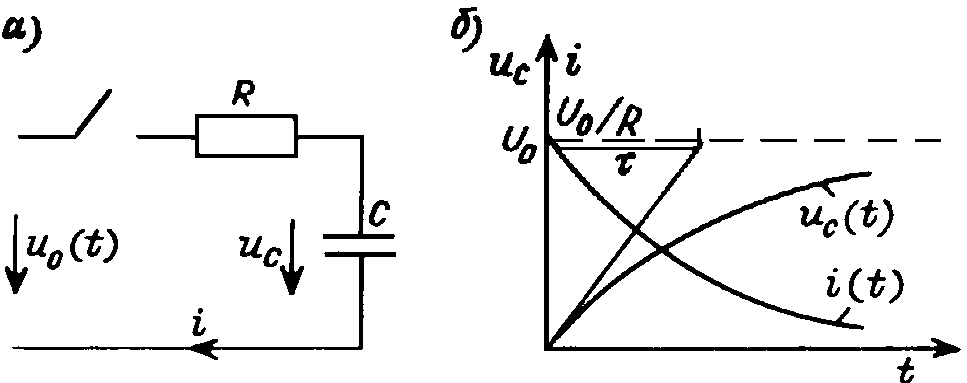
15.2. ПЕРЕХОДНЫЕ ПРОЦЕССЫ В ПРОСТЕЙШЕЙ RC-ЦЕПИ

При анализе подключения RC-цепи к источнику напряжения u₀(t) (рис. 15.1, а), согласно сказанному выше, из уравнений, составленных для цепи после коммутации, —  

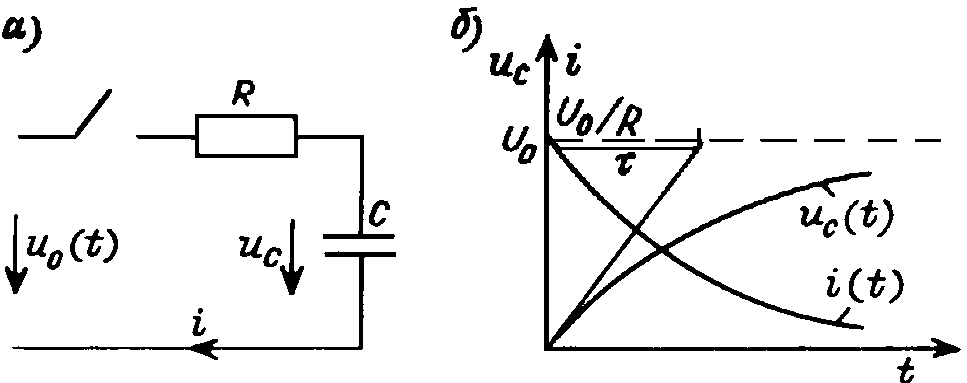
Рис. 15.1

при замкнутом ключе

исключим ток и сведем их к одному уравнению относительно переменной состояния u_C:

Общее решение полученного неоднородного дифференциального уравнения имеет вид суммы частного решения неоднородного и общего решения однородного уравнений

Для нахождения второго из них составим характеристическое уравнение RCl + 1 = 0, корнем которого является l = – 1/RC. Общее решение однородного уравнения — свободная составляющая напряжения u"_C — соответствует цепи с исключенным источником

где A — пока неопределенная константа; t = RC — величина, имеющая размерность времени, характеризующая скорость протекания переходного процесса, так называемая постоянная времени.

Характер частного решения — вынужденной составляющей u'_C — определяется видом воздействующего на цепь напряжения источника u₀(t). В простейших случаях  подключения цепи к постоянному источнику u₀(t) = U₀ = const и замыкания конденсатора на резистор, когда u₀(t) = 0, составляющую u'_C можно найти, руководствуясь следующими соображениями. Вид общего решения u_C = u'_C + A e^–t/t показывает, что u'_C представляет собой значение напряжения на конденсаторе, которое будет достигнуто в установившемся режиме после окончания переходного процесса. Действительно, при t ®  ¥ u_C(t) ®  u'_C, так как свободная составляющая u"_C с течением времени затухает. Рассмотрим перечисленные случаи.

1. Заряд конденсатора от источника постоянного напряжения u₀(t) = U₀. К концу переходного процесса на конденсаторе установится напряжение источника U₀, т. е. u'_C = U₀. Отсюда

Для определения постоянной A используем начальное условие. Согласно закону коммутации, напряжение на конденсаторе в момент замыкания ключа остается непрерывным. Поэтому если в исходном состоянии до замыкания ключа конденсатор не был заряжен (u_C(– 0) = 0), то это же нулевое значение u_C сохранит и непосредственно после замыкания. Из последнего выражения при t = 0 имеем

Отсюда найдем A = – U₀ и запишем окончательно

u_C(t) = U₀(1 - e^-t/t).

Из исходных уравнений цепи получим для тока:

Характер изменения тока и напряжения при подключении RC-цепи к источнику постоянного напряжения изображен на рис. 15.1, б.

Значение тока, содержащее лишь свободную составляющую, максимально в начальный момент времени, когда оно скачком достигает значения U₀/R, и все напряжение источника приложено к резистору. По мере зарядки конденсатора напряжение на нем повышается, это ведет к соответственному уменьшению тока в цепи. Скорость этих процессов определяется постоянной времени t. Она определяет время, за которое происходила бы зарядка конденсатора, если бы скорость зарядки сохранялась постоянной и равной ее значению в начале процесса (см. рис. 15.1, б). Так как скорость зарядки замедляется по мере увеличения напряжения, то за время, равное постоянной времени t = t, свободные составляющие уменьшаются по сравнению со своим начальным значением в e »  2,718 раза. За время t = 3t свободные составляющие затухают в e³ »  20,09 раза, а за время t = 5t — в е⁵ »  148 раз.

2. Разряд конденсатора на резистор (рис. 15.2, а).

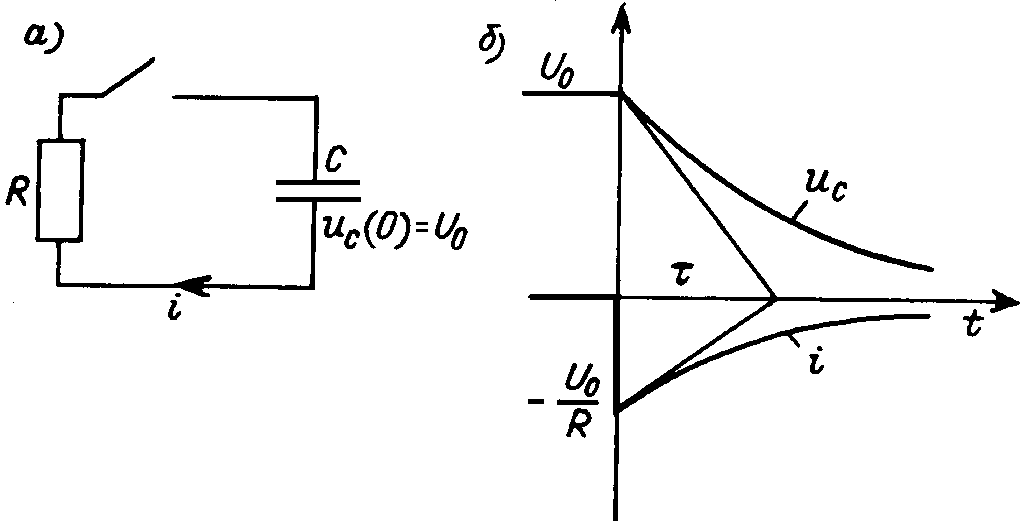
Рис. 15.2

Для расчета тока при разряде и напряжения u_C исходном уравнении следует положить u₀(t) = 0, что приводит его к однородному уравнению:

а напряжения и токи содержат лишь свободные составляющие. Поэтому его общее решение имеет вид

где константы A и t сохраняют прежний смысл.

Для определения значения A используем начальное условие — значение напряжения u_C(0) = U₀, до которого конденсатор был заряжен к моменту замыкания ключа. При t = 0 имеем

и окончательно для напряжения u_C запишем

Значение тока разряда определим из исходных уравнений

Соответствующие кривые изображены на рис. 15.2, б. Напряжение на конденсаторе непрерывно в момент коммутации и уменьшается по экспоненциальному закону от начального значения U₀. Скорость протекания разряда определяется постоянной времени t = RC.

3. Включение RL-цепи к источнику синусоидального напряжения u₀(t) = U_m0 sin (wt + y). В этом случае общие уравнения переходного процесса сохраняются; для напряжения u_C имеем уравнение

Его общее решение имеет ту же форму, что и ранее:

Теперь для определения частного решения u'_C рассмотрим установившийся синусоидальный процесс при t ®  ¥, когда свободная составляющая u"_C исчезает. Для определения напряжения u'_C(t) воспользуемся комплексным методом. Передаточная функция рассматриваемой цепи

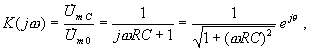
где q = – arctg (wRC), а амплитуда напряжения источника . Множитель, учитывающий начальную фазу y, здесь не опущен, так как за начало отсчета t = 0 принимается момент коммутации — замыкания ключа, а фаза y в этот момент может иметь произвольное значение.

Запишем далее выражение комплексной амплитуды напряжения на конденсаторе

и его мгновенное значение u'_C(t)

где  — амплитуда установившегося напряжения на конденсаторе. Теперь для определения значения постоянной A в общем решении имеем условие

Если в момент включения конденсатор не был заряжен, то

Это позволит записать окончательно

Значения тока в цепи определим дифференцированием

где I_m = U_mCwC — амплитуда тока в цепи в установившемся режиме.

Оба выражения для u_C и i в общем случае имеют периодическую вынужденную (первое слагаемое) и апериодическую свободную составляющие (второе слагаемое). При этом характер переходного процесса существенно зависит от двух факторов — начальной фазы напряжения источника в момент включения y и соотношения частоты w и параметров цепи, выражаемого безразмерным множителем wt = wRC = R/X_C. Проанализируем характерные ситуации.

Если в выражении для постоянной A аргумент синуса y + q = y – arctg wt равен нулю, то и A = 0, т. е., если включение цепи при нулевом начальном условии производится в момент, когда y = arctg wt, то переходный процесс в цепи вообще не возникает, а сразу устанавливается синусоидальный режим. 

С другой стороны, влияние начальной фазы в момент включения на процесс наиболее сильно, если рассмотренный аргумент синуса y + q = p/2. В этом случае апериодическая составляющая максимальна, и выражения для u_C и i после преобразования тригонометрических функций принимают вид:

Соответствующие зависимости изображены на рис. 15.3, а,б, где также отдельно приведены периодическая u'_C и апериодическая u"_C составляющие. Последняя построена для двух значений параметра wt.

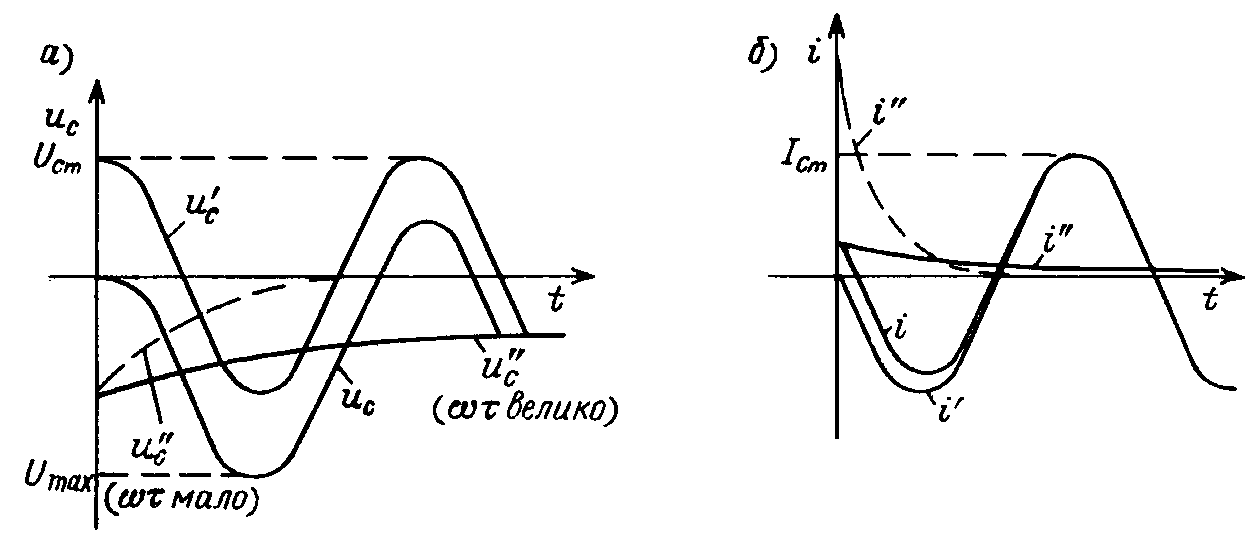
Рис. 15.3

При больших wt влияние апериодической составляющей существенно в течение ряда начальных периодов процесса — результирующая кривая напряжения на конденсаторе u_C имеет несимметричное относительно оси абсцисс расположение экстремумов, которые постепенно приближаются к симметричной кривой u'_C установившегося режима. Вследствие этого экстремальные значения этого напряжения u_max в начальные периоды могут превышать амплитуду установившегося значения. Это наиболее сильно проявляется в первом полупериоде. Так, при wt = p (или t = p/w) имеем u_C(p/w) = U_mC(– 1 – e^–p/wt), т. е. | u_max |/U_mC @  1 + e^–p/wt. Отсюда следует, что максимальное значение u_max не может превысить амплитуду установившегося режима U_mC более чем в два раза.

Если же, наоборот, значение wt малó — постоянная времени существенно меньше периода, то оказывается заметным всплеск тока в момент включения, показанный на рис. 15.3, б штриховой линией. Согласно приведенному выше выражению для i(t), этот всплеск может многократно превысить амплитуду установившегося тока: i(0) = I_m/wt. Однако этот начальный всплеск тока является кратковременным — он затухает в течение первого полупериода. Этот факт необходимо учитывать при подключении конденсаторов, обладающих весьма малым сопротивлением R, к источникам синусоидального напряжения, имеющим также малое внутреннее сопротивление (например, к сети). При других значениях начального значения напряжения источника в момент включения — при 0 < y + q < p/2 — начальные всплески тока и напряжения выражены не столь резко.