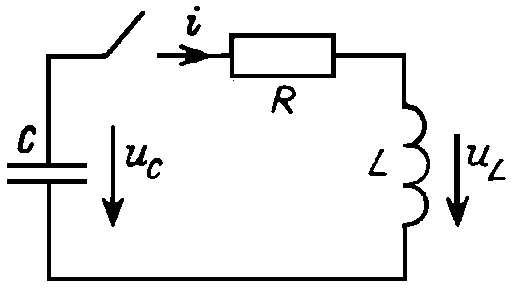
Рис. 15.8
Запишем уравнения переходного процесса в контуре
![]()
Исключая из приведенной системы uC, придем к дифференциальному уравнению 2-го порядка относительно тока
15.5. РАЗРЯД КОНДЕНСАТОРА В КОЛЕБАТЕЛЬНОМ КОНТУРЕ
Одна из классических задач расчета переходных процессов — анализ разряда конденсатора на цепь с последовательным соединением резистора и катушки (рис. 15.8).
|
Рис. 15.8 |
Запишем уравнения переходного процесса в контуре
Исключая из приведенной системы uC, придем к дифференциальному уравнению 2-го порядка относительно тока |
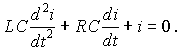
Характеристическое уравнение последовательного колебательного контура
| (15.1) |
имеет корни
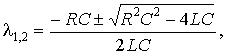
которые в зависимости от соотношений между параметрами цепи могут быть:
1) вещественными различными (R > 2ЦL/C);
2) вещественными равными (R = 2ЦL/C);
3) комплексно-сопряженными
(R < 2ЦL/C).
В первых двух случаях переходный процесс носит апериодический характер: разрядный ток не изменяет направления в течение всего процесса; в третьем случае процесс разряда колебательный.
При различных корнях (первый и третий случаи) общее решение однородного дифференциального уравнения можно записать в виде
![]()
Для определения двух постоянных интегрирования используем два начальных условия, вытекающих из условия непрерывности обеих переменных состояния в момент коммутации: i(0) = 0; uC(0) = U0. Из второго уравнения исходной системы можно найти значение производной di/dt в момент времени после коммутации. При t = + 0 di/dt = – U0/L. Из общего решения для значения тока и его производной при подстановке получим систему для определения постоянных интегрирования:
![]() ,
,
решение которой приводит к значениям постоянных
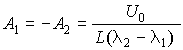
и позволяет записать выражение для тока, удовлетворяющее начальным условиям:
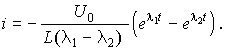 .
.
Напряжение uL имеет общее выражение
а для напряжения на конденсаторе uC получим из второго уравнения исходной системы
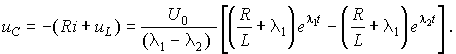
При его преобразовании учтем, что из характеристического уравнения по теореме Виета следует l1 + l2 = – R/L. Это позволяет привести последнее выражение к виду
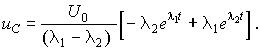
Ход разряда конденсатора существенно зависит от вида корней характеристического уравнения.
1. Апериодический разряд наблюдается при вещественных корнях l1, 2, что имеет место при соотношении между параметрами цепи R > 2ЦL/C.
Пусть l1 — меньший по абсолютному значению корень, к которому в формуле для корней относится знак “плюс” перед радикалом. При этом разность l1 – l2 в знаменателе выражения для тока положительная. Разность экспонент el1t – el2t также положительна, поскольку el1t убывает медленнее, чем el2t. Поэтому ток разряда сохраняет неизменное направление, противоположное направлению при заряде конденсатора. Поскольку i(0) = 0, в начале процесса — на фронте импульса — ток нарастает по абсолютному значению, а затем уменьшается (рис. 15.9).
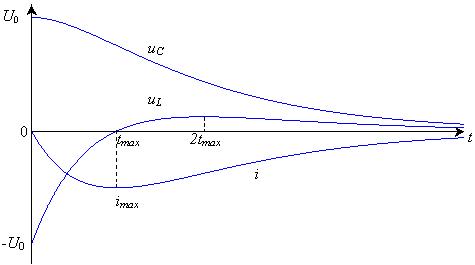
Рис. 15.9
Начальная скорость нарастания тока
di/dt(0) = |U0/L| определяется значением индуктивности
L. С ее уменьшением длительность фронта импульса сокращается, а абсолютное значение максимума
imax возрастает. Напряжение на индуктивности нарастает от значения – U0 при t = 0,
переходит через нуль в момент tmax достижения током максимального значения и изменяет знак.
Анализ зависимости
i(t) на экстремум показывает, что tmax
= ![]() . Напряжение на конденсаторе
uC имеет в течение всего процесса монотонный спадающий характер. Сначала его спад происходит медленно, далее в окрестности максимума тока убывание
uC ускоряется, а затем вновь замедляется. Из условия баланса напряжений в контуре
uC = – (Ri + L di/dt) легко установить связи между напряжениями на отдельных элементах и током в контуре. Так, в начальный момент разряда
uC = U0; uL = – U0; i = 0.
В момент максимума тока tmax uC = – Ri, а
uL = 0; в течение всего процесса имеем
uC > | uL|, так как Ri < 0.
. Напряжение на конденсаторе
uC имеет в течение всего процесса монотонный спадающий характер. Сначала его спад происходит медленно, далее в окрестности максимума тока убывание
uC ускоряется, а затем вновь замедляется. Из условия баланса напряжений в контуре
uC = – (Ri + L di/dt) легко установить связи между напряжениями на отдельных элементах и током в контуре. Так, в начальный момент разряда
uC = U0; uL = – U0; i = 0.
В момент максимума тока tmax uC = – Ri, а
uL = 0; в течение всего процесса имеем
uC > | uL|, так как Ri < 0.
2. Критический разряд. Характер всех рассмотренных зависимостей (при кратных корнях l1 = l2 = l = – R/2L) сохраняется. Решение для тока получим из общей формулы, раскрывая неопределенность при l1 = l2 = l
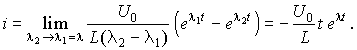
Для напряжений на индуктивности и емкости найдем:
![]()
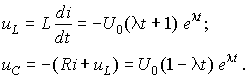
Из приведенных выражений следует, что,
как и при апериодическом разряде, значение тока в течение всего процесса отрицательно, напряжение uL изменяет знак
в момент максимума тока tmax = – 1/l = 2L/R =![]() , а напряжение на емкости имеет монотонный падающий характер.
, а напряжение на емкости имеет монотонный падающий характер.
3. Колебательный разряд наблюдается при комплексно-сопряженных корнях характеристического уравнения (при
R < 2ЦL/C
или
добротность контура Q > 0,5). Выражая корни через их вещественные и мнимые части
l1, 2 = – d ±
jw' (d = – R/2L; w' = ![]() ), преобразуем общие соотношения для i, uL и
uC:
), преобразуем общие соотношения для i, uL и
uC:
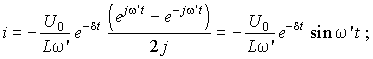
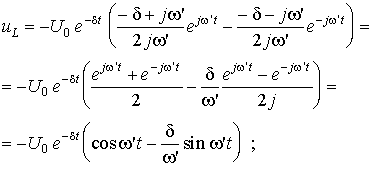
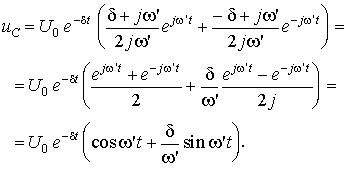
В этих преобразованиях использованы формулы Эйлера. Соотношения показывают, что все три переменные имеют при разряде колебательный характер, периодически изменяя знак. Период колебаний T определяется из условия изменения аргумента тригонометрических функций на 2p: 2p = w'T, откуда
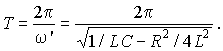
Период колебаний в контуре без потерь равен T0 = 2pЦLC. Затухание колебаний по амплитуде, определяемое экспоненциальными множителями e– dt, зависит от соотношения параметров контура. Обычно эта величина количественно характеризуется декрементом колебания D, равным отношению двух последующих амплитуд одного знака, отстоящих друг от друга на период D = e– dt/e– d(t+T) = edT. Вводится также понятие логарифмического декремента колебаний ln D = dT. У высокодобротного контура затухание имеет малое значение, вычитаемое в подкоренном выражении для периода T также мало, и T » T0 = 2pЦLC. При этом ln D = (R/2L) 2pЦL/C = pR/ЦL/C = pd = p/Q, где d = R/ЦL/C = 1/Q – затухание контура. Этим определяется смысл понятия затухания, которое при сделанных допущениях, практически выполняющихся при d < 0,2, пропорционально логарифмическому декременту колебаний. При этих значениях параметров, что соответствует D < 2, частота собственных колебаний контура w' практически равна его резонансной частоте w' » w0 = 1/ЦLC. Зависимости i, uL и uC(t) для D = 2 изображены на рис. 15.10.
Рис. 15.10
Начальная часть процесса (при t < T/4) имеет характер, сходный с начальной частью апериодического разряда. Однако теперь к моменту максимума тока t » T/4 катушка успевает накопить бóльшую часть энергии, первоначально запасенной в конденсаторе, который к этому времени уже почти разряжен. Далее, по мере спада тока, во второй четверти периода (T/4 < t < T/2) конденсатор перезаряжается, но напряжение на нем изменяет полярность на противоположную, а накопленная в катушке энергия вновь возвращается к конденсатору. Этот периодический обмен энергией продолжается и в последующие фазы разряда, но его интенсивность постепенно ослабевает, так как в течение каждого цикла перезарядки часть энергии рассеивается в виде тепла в сопротивлении контура R.