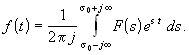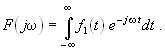
19.1. ЧАСТОТНЫЙ МЕТОД РАСЧЕТА ПЕРЕХОДНЫХ ПРОЦЕССОВ
Принципиально отличным методом расчета переходных процессов является частотный. Он не требует составления дифференциальных уравнений цепи, а базируется на использовании интегрального преобразования Фурье. Его первый этап — нахождение спектральной плотности — Фурье-изображения входного сигнала f1(t)
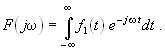
Далее в частотной области с помощью передаточной функции находят изображение выходной величины
![]()
затем временную зависимость выходного сигнала f2(t) определяют с помощью обратного преобразования Фурье
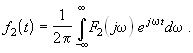
При анализе переходных процессов принимают, что входное воздействие прикладывается к цепи в момент времени t = 0, а предысторию процесса учитывают с помощью начальных условий — значений переменных состояния в начальный момент времени. Такая формулировка не охватывается изложенной схемой расчета, так как в ней отсутствует информация о начальных условиях. Поэтому с помощью интеграла Фурье можно рассматривать лишь переходные процессы при нулевых начальных условиях, когда входное воздействие f1 прикладывается к цепи, не имеющей начального запаса энергии, а при t < 0 все токи и напряжения равны нулю, т.е.
f1(t) = 0 и f2(t) = 0 при t < 0.
При анализе таких процессов формулы прямого и обратного преобразования Фурье принимают вид:
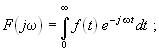 |
(19.1) |
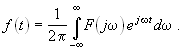 |
(19.2) |
Они определяют так называемое одностороннее преобразование Фурье. Ряд его свойств совпадает со свойствами двустороннего преобразования Фурье. Так, сохраняют силу свойства линейности, соотношения для изображения запаздывающего сигнала (см. п. 11.3). Выражения для Фурье-изображений наиболее часто встречающихся функций приведены в Приложении 4.
Поскольку частотный метод применяют преимущественно к цепям сложной структуры, для которых передаточную функцию, в частности, можно определить экспериментально, обратное преобразование Фурье обычно находят численным интегрированием. В этом случае целесообразно перейти от комплексной формы интеграла (19.2) к вещественной форме. Свойства четности вещественной части Fв и модуля F спектральной плотности F(± jw) = Fв(w) ± jFм(w) = F(w)e±jj(w) и нечетности мнимой части Fм и аргумента j(w) позволяют привести интеграл обратного преобразования к вещественной форме
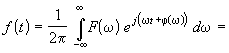
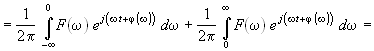
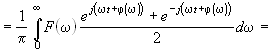
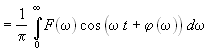 .
.
Рассмотрим далее выражение для выходного сигнала f при ± t, то есть при t > 0 и t < 0. Из последнего интеграла получим
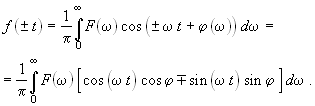 |
(19.3) |
Так как при t < 0 f(t) = 0, из полученного выражения следует, что для одностороннего преобразования Фурье имеем
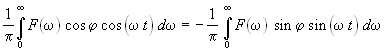 ,
,
или
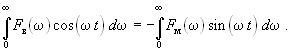
С учетом этой связи выражения для выходного сигнала f2(t) (19.3) при t > 0 можно представить целиком либо через вещественную, либо через мнимую часть спектральной плотности
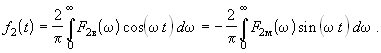
Помимо невозможности применения метода при ненулевых начальных условиях, его недостатком является ограничение, связанное с тем, что для многих практически важных сигналов преобразование Фурье в строгом математическом смысле не существует. Напомним, что для его существования требуется абсолютная интегрируемость функции f(t), которому не удовлетворяют, в частности, включаемый при t = 0 и неограниченно долго действующий постоянный или аналогичный синусоидальный сигналы.
Указанное ограничение можно снять следующим образом. Включим в формулу прямого одностороннего преобразования Фурье (19.1) дополнительный множитель e–st (s – положительная вещественная константа), обеспечивающий сходимость интеграла при ![]() :
:
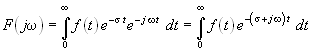 .
.
Перепишем аналогично формулу обратного Фурье-преобразования:
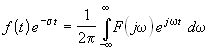 ,
,
или
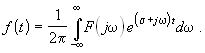
В полученных выражениях роль переменной частоты w теперь выполняет комплексная переменная s + jw. Обозначим ее единым символом s и, переходя к интегрированию по этой новой переменной в интеграле обратного преобразования, запишем обе формулы в виде:
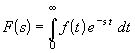 ;
;