Интегрирование уравнений состояния позволяет получить точные количественные данные о динамике процессов в цепи — найти зависимости от времени токов и напряжений на отдельных элементах. Поскольку для нелинейной цепи эти результаты имеют частный характер, так как отвечают вполне определенным значениям параметров элементов цепи и начальным условиям. Часто при анализе цепи нас интересуют качественные результаты — оценки характера процесса (например, колебательный или апериодический), его асимптотики при t ® ¥, существование периодических режимов. Если в линейной цепи подобные оценки выполняют на основе общих решений дифференциальных уравнений (например, с помощью анализа расположения корней характеристического уравнения), то в нелинейной цепи это, как правило, невозможно.

Для качественного анализа нелинейных цепей применяют метод фазового пространства. На его координатных осях откладывают текущие значения переменных состояния анализируемой цепи. Их изменению во времени соответствуют определенные кривые — фазовые траектории — в пространстве переменных состояния. Совокупность всех фазовых траекторий — фазовый портрет цепи — представляет исчерпывающее описание всех ее возможных режимов. Однако, в общем случае получение такого полного описания произвольной цепи представляет сложную задачу, так как фазовые траектории являются кривыми в многомерном пространстве.

Для автономных цепей 1-го порядка, в которых действуют источники, не зависящие от времени, на осях фазовой плоскости откладывают значения переменной состояния x (ось абсцисс) и ее производной по времени dx/dt (ось ординат). Фазовая траектория такой цепи полностью определена ее уравнением состояния

.

Это позволяет отразить все процессы в цепи при любых начальных условиях с помощью единственной фазовой траектории, построение которой не требует ни интегрирования уравнения состояния, ни каких-либо дополнительных преобразований.

Изменение переменных x и y на фазовой плоскости подчиняется следующим закономерностям. Так, в верхней полуплоскости y = dx/dt > 0, следовательно, x в ходе процесса растет, и изображающая точка движется по фазовой траектории слева направо. В нижней полуплоскости, наоборот, dx/dt < 0, и движение по фазовой траектории происходит справа налево, так как x убывает. Точки равновесия, соответствующие установившимся состояниям цепи, характеризуются нулевыми значениями: dx/dt = 0, или y = f(x) = 0 — находятся на пересечении фазовой траектории с осью абсцисс. Известно, что в нелинейной цепи возможно несколько состояний равновесия, поэтому фазовая траектория такой цепи может пересекать ось абсцисс в нескольких точках. Замкнутая фазовая траектория изображает периодический процесс и может пересекать ось абсцисс только вертикально.

Для построения фазовой траектории простейшей цепи с нелинейным конденсатором (рис. 30.1, а), описываемой системой уравнений:

,

приведем ее к одному уравнению относительно переменной состояния :

.

Фазовая траектория процесса в линейной цепи имеет вид прямой 1 (рис. 30.1, б).

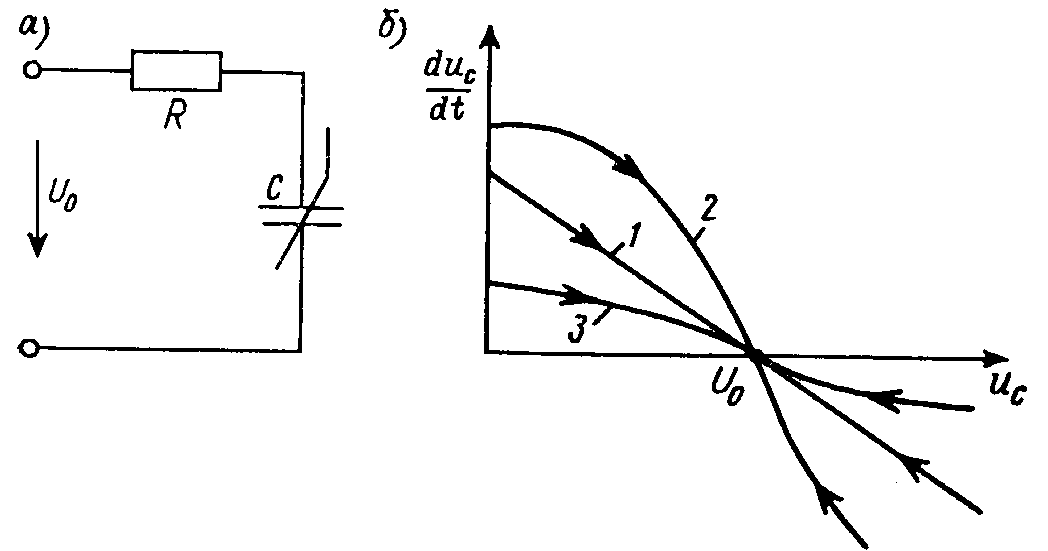
Рис. 30.1

Если дифференциальная емкость C_д уменьшается с ростом u_C, то фазовая траектория проходит выше, чем прямая для линейной цепи (кривая 2). Если, наоборот, ¶C_д/¶u_C > 0, то фазовая траектория имеет вид кривой 3. Все возможные фазовые траектории рассматриваемой цепи заканчиваются в одной и той же точке равновесия u_C = U₀, так как окончательное значение напряжения на конденсаторе не зависит от емкости конденсатора и характера ее изменения в переходном процессе.

Из приведенных графиков следует, в частности, что фазовая траектория непосредственно не дает информации о временном ходе переходного процесса: мы не можем ответить на вопрос о том, к какому моменту времени будет достигнуто то или иное значение напряжения u_C. Однако мы видим, что во всех изображенных на рис. 30.1, б случаях переходный процесс имеет монотонный характер: в зависимости от начального условия напряжения u_C либо возрастает (u_C < U₀), либо уменьшается (u_C > U₀). Можно также сделать вывод, что при ¶C_д/¶u_C < 0  (кривая 2) конденсатор заряжается быстрее, чем в линейном случае. Если C_д увеличивается по мере зарядки конденсатора, то переходный процесс замедляется (кривая 3).

Следует отметить, что всем переходным процессам, возникающим в цепи 1-го порядка с фиксированными параметрами при различных условиях, отвечает одна фазовая траектория, поэтому зависимость y = f(x), выражающая эту фазовую траекторию, дает полную информацию о характере процессов в цепи 1-го порядка при любых возможных начальных условиях.

Для автономных цепей 2-го порядка на координатных осях фазовой плоскости изображают две переменных состояния x₁и x₂, связанные системой уравнений:

,

и фазовые траектории представляют плоские кривые. Их характер имеет много общего с рассмотренным выше для цепи первого порядка, когда одно из уравнений записанной системы имеет вид  x₂ = dx₁/dt  (что часто встречается на практике, например, в цепях с последовательным или параллельным соединением катушки и конденсатора). Однако для цепи 2-го порядка построение фазовых траекторий требует исключения времени из уравнений состояния: разделив одно уравнение на другое, получим уравнение траекторий

.

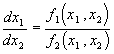Поскольку это уравнение дифференциальное, то на фазовой плоскости ему соответствует множество фазовых траекторий, каждой из которых отвечают определенные начальные условия x₁(0), x₂(0) (рис. 30.2).

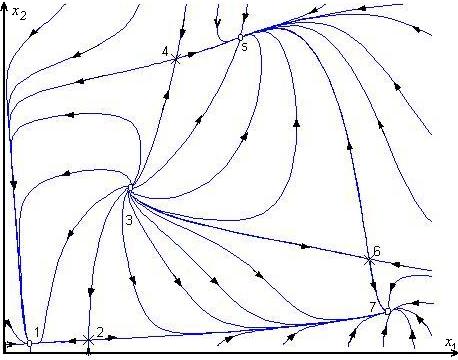
Рис. 30.2

Через каждую точку плоскости (x₁, x₂) проходит одна, вполне определенная траектория, что определяется однозначным ходом процесса при данных начальных условиях. В отдельных особых точках фазовой плоскости, соответствующих положениям равновесия, для которых соблюдаются условия  f₁(x₁, x₂) = f₂(x₁, x₂) = 0, сходятся или расходятся различные фазовые траектории.

Для изучения характера фазовых траекторий цепи второго порядка вблизи особых точек линеаризуем уравнения состояния в окрестности точки равновесия:

,

где a_ik = df_i/dx_k — производные, вычисленные в точке равновесия с координатами x₁₀, x₂₀, Dx₁= x₁- x₁₀, Dx₂= x₂ - x₂₀.

Ход процесса при малом отклонении от точки равновесия определяется корнями линеаризованного характеристического уравнения

.

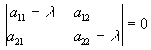Известно (см. п.23.1), что в зависимости от расположения корней l_1,2 на комплексной плоскости характер поведения системы может быть различным:
1) незатухающий колебательный  (l_1,2 = ± jw — чисто мнимые корни);
2) затухающий колебательный (l_1,2 = d ± jw — комплексные корни в левой полуплоскости);
3) нарастающий колебательный (l_1,2 = d ± jw — комплексные корни в правой полуплоскости);
4) затухающий апериодический (l_1,2 < 0 — оба вещественных корня в левой полуплоскости) — точки 1, 5 и 7 на рис. 30.2;
5) нарастающий апериодический (l_1,2 > 0 — оба корня вещественные, положительные)— точка 3 на рис. 30.2.

Вид фазовых траекторий в окрестности точки равновесия во всех перечисленных случаях и соответствующее расположение корней изображены на рис. 30.3, а-д.

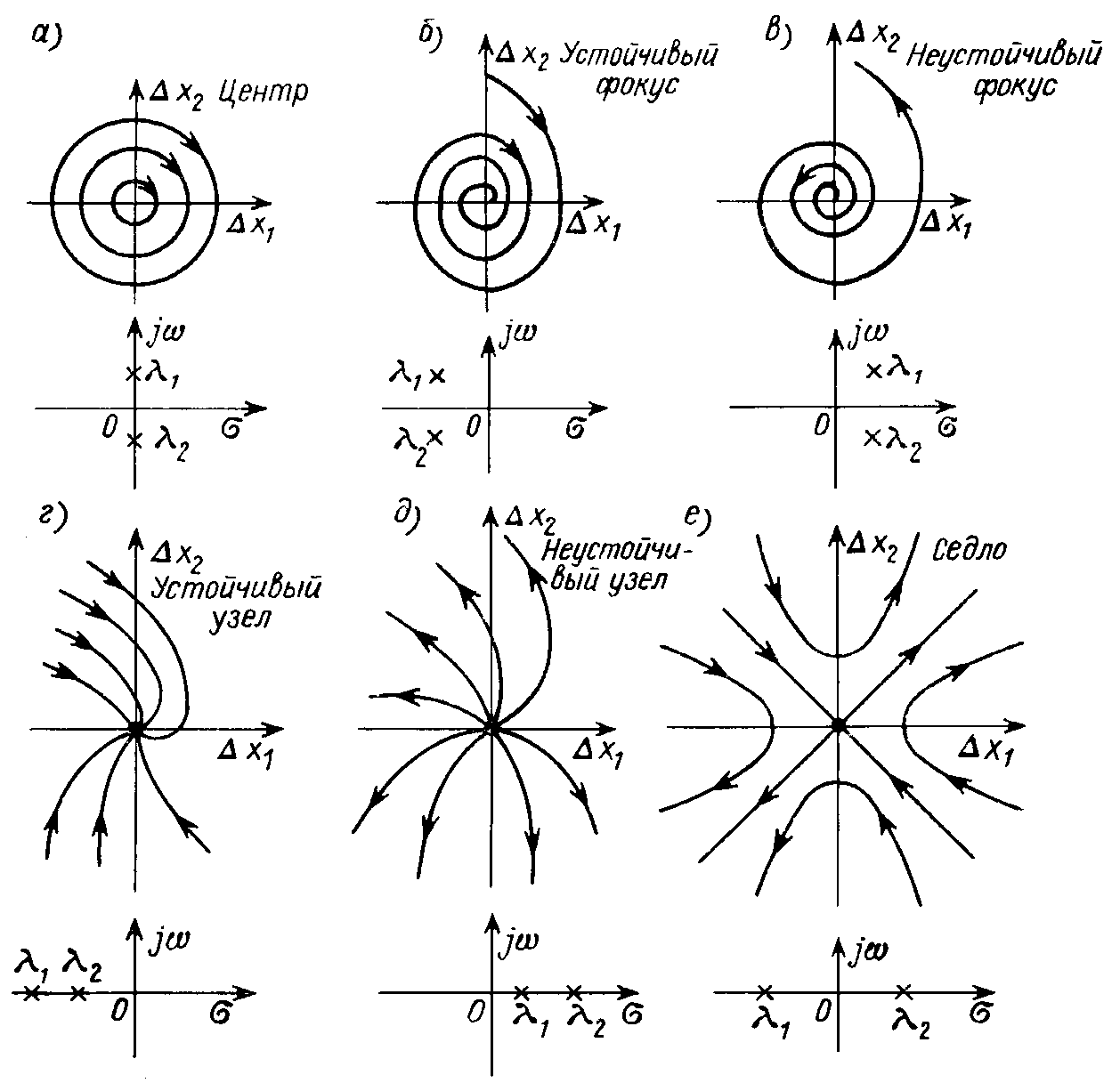
Рис. 30.3

Еще один тип точки равновесия — седло, которому отвечает один положительный, а другой отрицательный корень ; (точки 2, 4 и 6 на рис. 30.2 и рис. 30.3, е). Седловая точка равновесия является неустойчивой: отдельные фазовые траектории входят в нее, а другие — выходят. Периодическим процессам на фазовой плоскости отвечают замкнутые фазовые траектории — предельные циклы. Они устойчивы, когда отдельные фазовые траектории внутри и вне цикла притягиваются к нему (рис. 30.4). Предельный цикл, от которого траектории расходятся, будет неустойчивым.

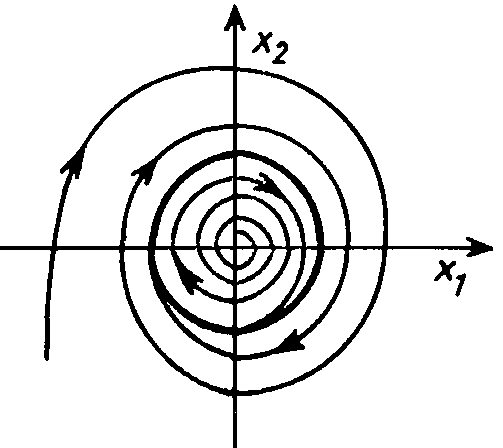
Рис. 30.4

Весь фазовый портрет системы 2-го порядка разбивается предельными циклами и сепаратрисами — траекториями, проходящими через седловые точки, — на области притяжения — аттракторы — отдельных устойчивых состояний (фокусов, узлов и предельных циклов). Поэтому в зависимости от начальных условий процесс в цепи 2-го порядка может стремиться к тому или иному устойчивому предельному состоянию. Эта особенность характерна именно для нелинейных цепей — в линейных цепях предельное состояние не зависит от начальных условий.