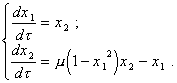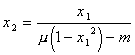30.5. НЕЛИНЕЙНЫЕ АВТОКОЛЕБАТЕЛЬНЫЕ СИСТЕМЫ.
КВАЗИГАРМОНИЧЕСКИЕ
И РЕЛАКСАЦИОННЫЕ АВТОКОЛЕБАНИЯ
Ранее мы
установили существование
автоколебательных режимов в активных цепях
с обратными связями (п.
23.3). Анализ, выполненный в линейном
приближении, не позволял установить в этих
цепях амплитуду гармонических колебаний,
которая определяется нелинейными
свойствами элементов цепи, в частности,
усилителя. Поэтому полный анализ
автоколебаний следует проводить с учетом
нелинейных свойств таких цепей.
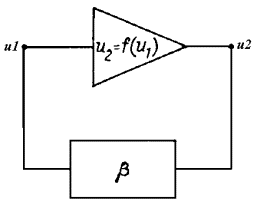
Рис. 30.13
|
Рассмотрим
автоколебательную активную цепь,
включающую усилитель с нелинейной
зависимостью выходного напряжения от
входного u2 = f(u1),
охваченный линейной цепью обратной
связи (рис. 30.13). Пусть она обладает
передаточной функцией b(s)
= U1(s)/ U2(s)
= s/(a0s2 + a1s
+ a2).
Такую передаточную функцию имеют цепи с
двумя динамическими элементами,
например, RC-цепи
(см. рис.
23.6, в-д), а также RLC-цепи
(см. рис.
23.8).
|
Коэффициенты a0,
a1
и a2 определяются
параметрами цепи обратной связи.
Передаточная функция b(s)
соответствует временной связи между
входным и выходным напряжениями
усилителя, которая выражается
дифференциальным уравнением
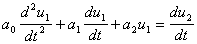 .
.
С
учетом нелинейной характеристики
усилителя выразим правую часть уравнения в
виде du2/dt = (df/du1)(du1/dt). Это приводит к
нелинейному дифференциальному уравнению
относительно u1:
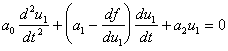 .
.
Напомним,
что в линейной цепи при df/du1
= k
= const генерация
синусоидальных колебаний имеет место при
обращении члена с первой производной du1/dt
в нуль. При нелинейной
зависимости u2 = f(u1)
условие a1
- df/du1
= 0 может выполняться
только для определенного фиксированного
значения u1
= const,
то есть оно не может соблюдаться в ходе
всего цикла автоколебаний, когда u1
является переменной величиной. Поэтому
автоколебания в нелинейной цепи не будут
иметь строго синусоидального характера.
Рассмотрим случай, когда коэффициент
усиления усилителя с повышением входного
напряжения уменьшается. Простейшую
аппроксимацию такой характеристики можно
выразить кубическим полиномом u2 = f(u1)
=
k0 - k1 u13,
в котором оба коэффициента k0
и k1
положительны. При такой аппроксимации для
производной df/du1
имеем квадратичную зависимость df/du1=
k0
- 3k1u12.
С учетом этой зависимости перепишем
уравнение для u1
в виде:
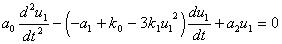
и
приведем его к безразмерному виду. Принимая
в качестве базисных величин 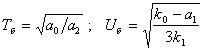 ,
получим
,
получим
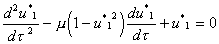 , , |
(30.1) |
где m =
(k0 - a1)/(a2Tб), u*1
= u1/U0, t = t/Tб
— безразмерные величины
Полученное
уравнение называется уравнением Ван-дер-Поля.
Таким образом, характер процессов в цепи
определяется безразмерным параметром m
Исследуем
сначала уравнение Ван-дер-Поля с помощью
фазовой плоскости. Принимая в качестве
фазовых переменных x1
= u*1; x2
= du*1/dt, запишем вместо
уравнения (30.1) систему уравнений в
нормальной форме:
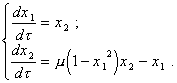
Для построения фазовых
траекторий воспользуемся методом изоклин.
Из последней системы найдем
дифференциальное уравнение, определяющее
фазовые траектории:
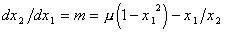
откуда получим
уравнения изоклин
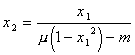
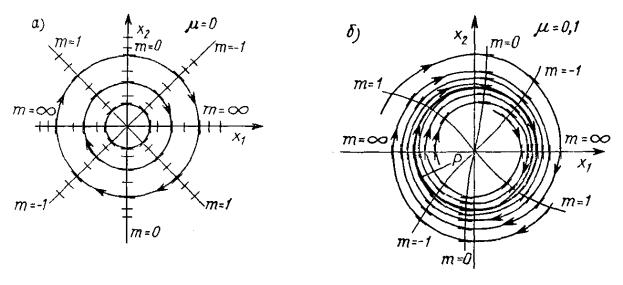
При m = 0 — в линейной
цепи без затухания — изоклины являются
прямыми, выходящими из начала координат (рис.
30.14, а), а фазовые траектории имеют вид
концентрических эллипсов. Эти траектории
замкнуты, что определяет автоколебательный
гармонический режим в линейной цепи.
Амплитуда незатухающих колебаний
определяется начальными условиями и не
зависит от свойств цепи.
|
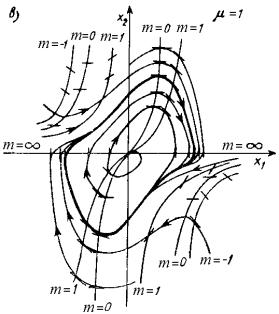
Рис.
30.14
|
Более
сложный характер имеют процессы в
нелинейной цепи. Степень влияния
нелинейности характеристики усилителя
определяется значением m, зависящим от
параметров цепи. При достаточно малых
напряжениях u*1
= x1
— в окрестности начала координат —
нелинейные свойства цепи проявляются
слабо, и при любых положительных m
в
начале координат имеет место
неустойчивый фокус, от которого фазовые
траектории расходятся в виде спиралей.
Анализ
характера изоклин, изображенных на рис.
30.14, б для значения m = 0,1,
показывает, что при больших начальных
значениях x1(0)
фазовые траектории имеют
свертывающийся характер. Это означает,
что область вблизи начала координат и
область удаления от него, разделены
замкнутой фазовой траекторией (точка Р
на рис. 30.14, б),
|
к которой сходятся все
остальные фазовые траектории как
изнутри, так и снаружи. Этот предельный
цикл является устойчивым и определяет
автоколебательный периодический режим,
который устанавливается в системе после
окончания переходного процесса.
Параметры
этого цикла позволяют определить амплитуду
и характер колебаний в системе. При малых
значениях параметра предельный цикл имеет
форму, близкую к эллиптической, что
соответствует синусоидальному характеру
автоколебаний. При больших значениях m
цикл деформируется, и
колебания приближаются к релаксационным (рис.
30.14, в). В этом случае их анализ можно
проводить численным интегрированием. При
малых значениях m для анализа колебаний,
близких к синусоидальным, можно
использовать метод медленно меняющихся
амплитуд, предложенный Ван-дер-Полем.
Дальше
Обратно к плану лекции

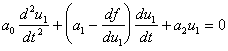 .
. 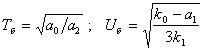 ,
получим
,
получим