Для математического описания способа соединения ветвей цепи и принадлежности их к контурам и сечениям используются матрицы соединений, контуров и сечений — прямоугольные матрицы, столбцы которых отвечают ветвям цепи, а строки — узлам, контурам и сечениям соответственно.

Матрица соединений A показывает, к какому узлу присоединены ветви направленного графа цепи. Если элемент матрицы a_jk = + 1, то это означает, что k-я ветвь присоединена к j-му узлу и направлена от него; a_jk = – 1 имеем для ветви k, присоединенной к j-му узлу и направленной к нему; a_jk = 0 имеем для k-й ветви, не присоединенной к узлу j.

Для мостовой цепи, направленный граф которой представлен на рис. 1.8, б, матрица соединений A_a имеет q = 4 строки и p = 6 столбцов:

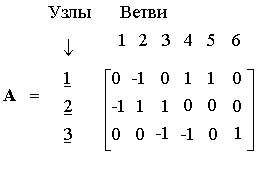
Матрица A_a содержит избыточную информацию. Так как каждая ветвь присоединена к двум узлам, то сумма элементов каждого столбца равна нулю. Поэтому последнюю, 4-ую строку можно однозначно восстановить по предыдущим. Обычно при записи матрицы соединений, обозначаемой просто A, избыточную, последнюю, строку опускают. Таким образом, полная матрица соединений A_a цепи с q узлами и p ветвями имеет размер q ´  p, а размер матрицы A – (q - 1) ´  p.

Матрица контуров B содержит информацию о том, в какие контуры цепи входят ветви. Здесь используют тот же принцип записи, что и для матрицы A: строки B-матрицы отвечают отдельным контурам цепи, столбцы — ветвям:

Матрица сечений D дает информацию о принадлежности ветвей цепи к определенным сечениям. Каждая строка ее отвечает одному ориентированному сечению цепи. Элементы строки, соответствующие, как и у матриц A и B, отдельным ветвям цепи, равны + 1, – 1 или 0 в зависимости от того, входит ли данная ветвь в рассматриваемое сечение или нет. Если направление k-й ветви, входящей в j-е сечение, совпадает с его ориентацией, то элемент матрицы сечений d_jk равен + 1, в противном случае он равен – 1; d_jk = 0 имеем для ветви, не входящей в данное сечение. Если каждое сечение охватывает лишь один узел цепи, матрица D совпадает с матрицей соединений A: D = A.

При составлении матриц B и D необходимо учитывать лишь существенную информацию о цепи, избегая включения данных о контурах и сечениях, информация о которых может быть получена по уже имеющейся в матрице. Иными словами, матрицы B и D составляют для так называемых независимых контуров и сечений. Например, для графа мостовой схемы (см. рис. 1.8, б), контуры ,‚ и ƒ образуют независимую систему. Соответствующая такому выбору контуров матрица B записывается в виде: