3.2. МАТРИЧНАЯ ЗАПИСЬ УЗЛОВЫХ УРАВНЕНИЙ
Будем рассматривать цепь как совокупность составных ветвей, включающих проводимости, идеальные источники ЭДС и тока (см. рис. 2.2, а,б), компонентные уравнения которых могут быть записаны в общей форме
![]()
где i, u, e, J — векторы токов, напряжений, источников ЭДС и тока составных ветвей; G = diag [G1, G2, ... , Gn] — диагональная матрица проводимостей ветвей.
Как и выше, предполагаем отсутствие вырожденных ветвей с идеальными источниками ЭДС (G = ¥). Ветви с идеальными источниками тока могут присутствовать в схеме, для них имеем G = 0.
Запишем первый закон Кирхгофа в матричной форме
![]()
Выразим далее вектор напряжений ветвей через вектор узловых напряжений следующим образом:
![]()
Действительно, строка транспонированной матрицы имеет не более двух ненулевых элементов (1 и – 1). Поэтому напряжение ветви с номером p, ориентированной от узла k к узлу m, выражается как разность up = uk0 – um0, так как p-я строка имеет лишь два ненулевых элемента apk = 1 и apm = – 1.
Полученная связь позволяет записать компонентное уравнение в виде
![]()
Его подстановка в матричное уравнение первого закона Кирхгофа и преобразования приводят к матричному узловому уравнению
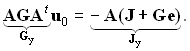
Таким образом, матрица узловых проводимостей выражается как двойное матричное произведение ![]() , а вектор узловых токов
, а вектор узловых токов ![]() .
.