8.1. ВХОДНЫЕ И ПЕРЕДАТОЧНЫЕ ФУНКЦИИ ЦЕПЕЙ СИНУСОИДАЛЬНОГО ТОКА
Применение комплексного метода сводит соотношения между мгновенными токами
i(t) и напряжениями u(t), выражаемые дифференциальными уравнениями, к алгебраическим соотношениям между их комплексными изображениями
I(jw), U(jw). Поэтому составленные для цепи уравнения в комплексной форме позволяют алгебраически выразить любой комплексный ток или напряжение – выходную величину
через входную величину
— напряжение или ток, подаваемые к входным зажимам:
где K(jw) — передаточная функция цепи, являющаяся рациональной дробью аргумента jw, коэффициенты полиномов числителя и знаменателя которой выражаются через параметры цепи. Передаточная функция является комплексным числом
модуль которого K(w) выражает отношение действующих значений (или амплитуд) выходного и входного сигналов, а ее аргумент q(w) определяет фазовый сдвиг между ними:
где y2 и y1 — начальные фазы обоих сигналов.
Размерность передаточной функции определяется размерностями связываемых ею величин. Если входная и выходная величины — напряжения (рис. 8.1, а), то передаточная функция K(jw) безразмерна; то же относится и к случаю, если обе величины являются токами (рис. 8.1, б). Если выходная величина — напряжение, а входная — ток (рис. 8.1, в), то говорят о передаточном сопротивлении Z12(jw) и наконец, соотношение между входным напряжением и выходным током определяет передаточная проводимость Y12(jw) (рис. 8.1, г).
Рис. 8.1.
Входные величины — комплексное сопротивление двухполюсника (рис. 8.2)
и входная проводимость 
также выражаются рациональными дробями аргумента
jw.
|
Рис. 8.2. |
Модулем комплексного входного сопротивления является полное сопротивление цепи
Z(w), его аргументом j(w) — фазовый сдвиг между напряжением и током, вещественная часть
R(w) — активное, а мнимая часть
X(w) — реактивное сопротивление.
Для комплексной входной проводимости аналогично имеем |
Y(jw) = y(w) e-jj(w) = G(w) - jB(w),
где y(w), G(w) и B(w) — полная, активная и реактивная проводимости цепи.
Определим входные и передаточные функции для цепи (рис. 8.3).
Рис. 8.3.
Выражая комплексные сопротивления ветвей
запишем входное сопротивление цепи:
Вещественная часть входного сопротивления пассивной цепи неотрицательна:
а его мнимая часть может быть как положительной, так и отрицательной
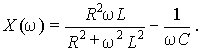
Получим выражение для передаточной функции рассматриваемой цепи по напряжению:
где ZLR = jwLR/(jwL + R) (при переходе к последнему выражению числитель и знаменатель дроби были умножены на wC).
Передаточная комплексная функция имеет модуль
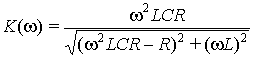
и аргумент
Амплитудные и фазные частотные характеристики. При анализе процессов преобразования сигналов электрическими цепями представляет интерес исследование зависимостей передаточных и входных функций рассматриваемой цепи от частоты. График частотной зависимости модуля передаточной функции называется амплитудно-частотной характеристикой, а график зависимости аргумента передаточной функции — фазочастотной характеристикой. Обе зависимости, построенные в широком частотном диапазоне, дают наглядное преобразование о характере преобразования сигналов данной цепью.
На рис. 8.4 по приведенным выше зависимостям построены частотные характеристики цепи рис. 8.3.
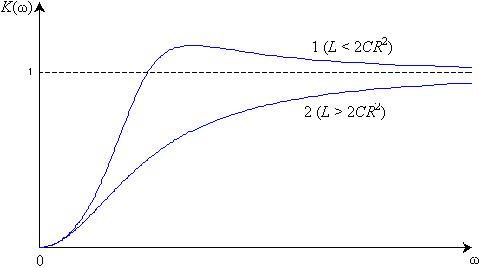
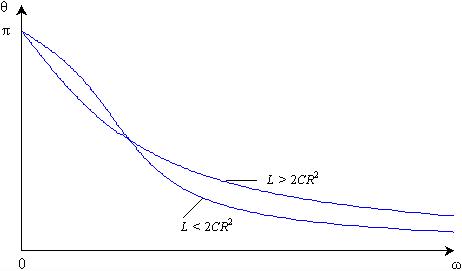
Рис. 8.4
Из них следует, что эта цепь пропускает преимущественно сигналы высоких частот. В зависимости от соотношения ее амплитудно-частотная характеристика имеет максимум (кривая 1), либо монотонно увеличивается от нулевого значения при w = 0 до K(w) = 1 при w ® ¥. Оба эти предельных режима легко проанализировать. При w = 0 (режим постоянного тока) конфигурация цепи упрощается, так как постоянный ток не протекает через конденсаторы, а индуктивности представляют для него нулевое сопротивление. Поэтому для определения передаточной функции на постоянном токе конденсаторы в схеме следует разомкнуть, а катушки — закоротить. Получим чисто резистивную цепь, анализ которой существенно проще. Аналогично при w ® ¥ сопротивления конденсаторов цепи стремятся к нулю, а сопротивления катушек неограниченно возрастают. Поэтому для анализа цепи при высоких частотах следует, наоборот, закоротить конденсаторы и разомкнуть катушки, что опять сводит задачу к расчету чисто резистивной цепи.
Примените сформулированные правила к анализу асимптотических режимов при w ® 0 и w ® ¥ в рассматриваемой цепи.
Существуют и другие способы представления частотных свойств передаточных функций: путем изображения частотных характеристик вещественной и мнимой частей K(jw) = Kв(w) + jKм(w) либо с помощью построения на комплексной плоскости кривой, которая отвечает совокупности значений K(jw), соответствующих различным частотам — амплитудно-фазовая частотная характеристика.
На рис. 8.5. изображена амплитудно-фазовая частотная характеристика передаточной функции цепи (рис. 8.3).
Рис. 8.5
Для ее построения при отдельных значениях частоты находят вещественную и мнимую части передаточной функции: Kв(w) = K(w) cos q; Kм(w) = K(w) sin q. Эти значения соединяют на комплексной плоскости непрерывной кривой, которая наглядно позволяет проследить характер изменения K(jw) при изменении w от нуля до бесконечности.
Аналогично изображают и частотные характеристики входных функций: сопротивления Z(jw) = R(w) + jX(w) = z(w)e jj(w) — его вещественной и мнимой частей R(w) и X(w), модуля z(w) и фазового сдвига j(w) или проводимости Y(jw).
