9.1. ЦЕПИ С ИНДУКТИВНО СВЯЗАННЫМИ ЭЛЕМЕНТАМИ. МАГНИТНЫЕ ЦЕПИ
Индуктивные элементы, находящиеся в общем магнитном поле, оказывают при изменении во времени протекающих по ним токов взаимное влияние друг на друга, которое наиболее существенно проявляется у близко расположенных или размещенных на общем сердечнике индуктивных катушек. Такие элементы электрических цепей называют индуктивно связанными.
Определение параметров подобных цепей требует анализа пространственного распределения магнитного поля, в общем случае проводимого методами теории электромагнитного поля. Однако в простейших случаях, в первую очередь, для обмоток на общих сердечниках, возможно упрощенное описание этого явления, основанное на приближенном представлении картины магнитного поля, которое принимается локализованным в объеме сердечника. В этом приближении связи между магнитными потоками в стержнях сердечника и вызывающими их токами могут быть описаны с помощью интегральных параметров магнитных цепей. Магнитные цепи — системы с сердечниками, магнитные потоки в стержнях которых создаются токами, протекающими в обмотках, расположенных на этих стержнях (рис. 9.1, а).
Рис. 9.1
Они подобны электрическим цепям, где токи, текущие по отдельным участкам, вызваны источниками ЭДС. Допущение о локализации магнитного поля в объеме сердечника, положенное в основу представления о магнитной цепи, выполняется тем точнее, чем выше магнитная проницаемость материала сердечника.
Расчеты магнитных цепей аналогичны расчетам токов в электрических цепях. Аналогия включает в себя как физические величины, так и связывающие их законы. Аналогом тока
i в электрической цепи является магнитный поток
Φ в магнитной цепи. Обе эти величины выражаются как поверхностные интегралы от плотности тока
J и магнитной индукции B, которые также аналогичны друг другу. Цепь аналогий продолжает напряженность электрического поля
E и напряженность магнитного поля H. В электрической цепи интеграл
по контуру равен сумме ЭДС, действующих в этом контуре. Соответствующая связь в магнитной цепи выражается законом полного тока
(wk — число витков обмотки;
ik — ее ток). Величина
ikwk в правой части последнего равенства называется магнитодвижущей силой (МДС).
Аналогом электрического напряжения
является МДС на участке цепи
. Отношение напряжения в электрической цепи к току
u/i = R имеет аналогом магнитное сопротивление участка
F/Φ = Rм. Для прямолинейного участка длиной
l с постоянным сечением s и постоянными по сечению значениями индукции
B и напряженности H можно записать:
где μa — абсолютная магнитная проницаемость материала сердечника.
Поэтому для магнитного сопротивления такого участка имеем
Подобно электрическим сопротивлениям, магнитные сопротивления последовательно включенных (обтекаемых одним магнитным потоком) участков магнитной цепи складываются.
Для расчета разветвленных магнитных цепей (как и электрических) используют законы Кирхгофа. Первый закон Кирхгофа выражает баланс магнитных потоков Φk, сходящихся к узлу магнитной цепи
В контуре магнитной цепи AmBnA действует второй закон Кирхгофа
т. е. суммарная МДС, создаваемая охватывающими контур обмотками, равна сумме МДС на участках цепи этого контура.
Сформулированные соотношения и законы позволяют рассчитать магнитную цепь любой сложности. Однако необходимо иметь в виду, что результаты расчетов магнитных цепей являются гораздо более приближенными, чем электрических цепей. Это вызвано:
рассеянием магнитного потока — непостоянством потока вдоль отдельных участков магнитной цепи, связанным с замыканием части силовых линий магнитного поля по воздуху, окружающему сердечник с обмоткой (линии потока рассеяния Φσ изображены на рис. 9.1, а штриховой линией),
нелинейностью свойств ферромагнитных материалов сердечников, магнитная проницаемость которых зависит от напряженности магнитного поля μа(H). Поэтому задача расчета магнитной цепи является нелинейной и требует последовательных приближений с уточнением значений магнитной проницаемости на отдельных участках цепи.
Расчет магнитных потоков в стержнях магнитной цепи рис. 9.1, а, аналогичен расчету электрической цепи рис. 9.1, б. Принимая ориентировочные значения μаk, соответствующие характеристикам намагничивания материала, находят магнитные сопротивления стержней 1 – 3: Rмk = lk/μаksk (k = 1, 2, 3). Поток, создаваемый обмоткой на первом стержне, разветвляется между вторым и третьим стрежнями, включенными параллельно. Поэтому для общего магнитного сопротивления рассматриваемой цепи имеем
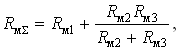
как и в соответствующей электрической цепи.
Магнитный поток в первом стержне равен Φ1 = iw/RмΣ. Потоки в параллельных стержнях распределяются обратно пропорционально их магнитным сопротивлениям:
При необходимости по найденным значениям потоков определяют магнитную индукцию на участках цепи Bk = Φk/sk, которая служит для уточнения значений μаk на участках, используемых при повторном расчете.
Связи между токами и напряжениями индуктивно связанных обмоток (рис. 9.2). Взаимное влияние индуктивно связанных обмоток проявляется в том, что при изменении тока i1 создаваемый им поток ΦM индуктирует ЭДС взаимоиндукции e2M = – dΨ2M/dt, где Ψ2M = w2ΦM — потокосцепление взаимоиндукции. Предполагая связь Ψ2M = M21i1 между потокосцеплением и вызывающим его током i1 линейной (взаимная индуктивность M21 = const), запишем выражение для ЭДС взаимоиндукции e2M в виде
Имеет место и обратное влияние — в первой катушке наводится ЭДС взаимоиндукции
Согласно принципу взаимности,
M12 = M21. В зависимости от направления токов в обмотках и пространственной ориентации обмоток потоки само- и взаимоиндукции
ΦL и ΦM в каждой обмотке могут либо складываться, либо вычитаться.
Рис. 9.2
В магнитной цепи рис. 9.2 эти потоки складываются, и для суммарных ЭДС, индуктированных в обеих обмотках, имеем
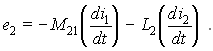
Для преодоления этих ЭДС во внешних цепях, к которым подключены обе обмотки, необходимо приложить напряжения:
|
(9.1) |
Однако используемое на схемах электрических цепей условное графическое изображение катушек не отражает их пространственной ориентации. Поэтому информацию об относительном направлении потоков само- и взаимоиндукции приходится задавать дополнительно. В связи с этим приняты следующие условные обозначения (рис. 9.3, а,б).
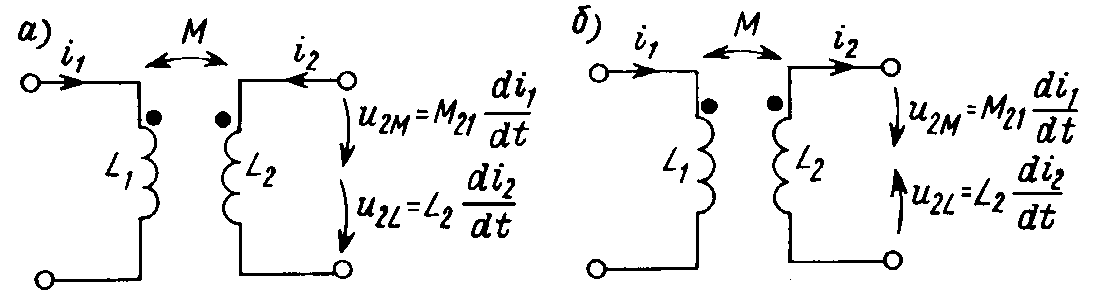
Рис. 9.3
Точки, отмечающие один из зажимов каждой катушки, имеют следующий смысл: при положительном направлении тока в первой катушке (от точки) составляющая напряжения u2M = M21 di1/dt, обусловленная взаимной индукцией, во второй катушке имеет положительное направление также от точки. Записанные выше соотношения для напряжения будут справедливы для схемы, изображенной на рис. 9.3, а либо при направлении токов в обеих катушках сверху вниз, либо снизу вверх. Маркировка зажимов катушек точками не предопределяет выбора положительных направлений токов в катушках. Так, при выборе других положительных направлений токов в тех же катушках (рис. 9.3, б) теперь запишем:
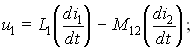
Направление отсчета напряжения мы принимаем соответствующим стрелке, указывающей на схеме принятое положительное направление тока в данной катушке. В отличие от собственной индуктивности L, которая всегда положительна, взаимная индуктивность M может быть положительной, отрицательной либо равной нулю. Для двух связанных катушек маркировку зажимов точками всегда можно выполнить так, чтобы она отражала их пространственную ориентацию при положительном значении M. Однако при трех и большем числе индуктивно связанных катушек потоки взаимоиндукции, обусловленные отдельными катушками, могут иметь неодинаковые направления. Это проще всего отразить, присвоив знак “минус” взаимным индуктивностям, обусловленным потоками взаимной индукции, направление которых противоположно направлению потока самоиндукции.
Соотношения между токами и напряжениями для двух обмоток очевидным образом обобщаются на системы с произвольным числом индуктивно связанных обмоток. Так, для трех обмоток имеем:
или в матричной форме
Здесь также, как и в предыдущем случае, взаимные индуктивности с попарно одинаковыми индексами равны друг другу.
