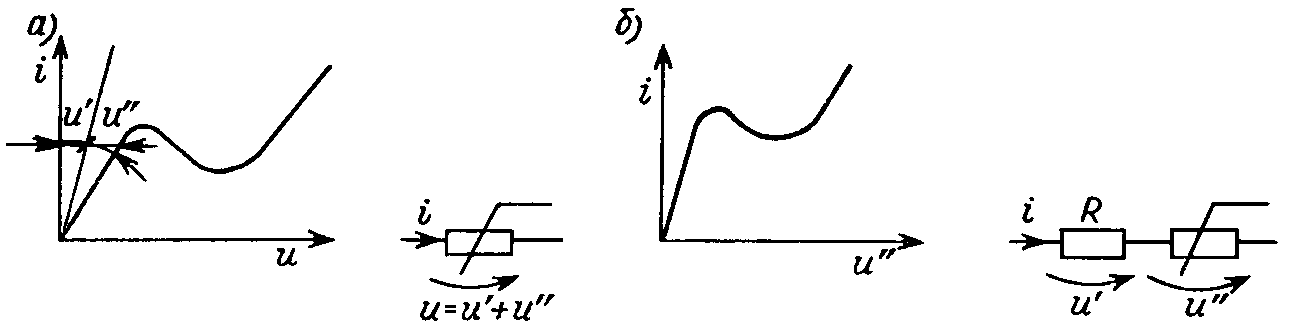
Система уравнений нелинейной резистивной цепи включает нелинейные компонентные уравнения и линейные уравнения, выражающие законы Кирхгофа для сечений и контуров цепи. Получение однозначного решения системы требует представления немонотонных характеристик, управляемых током, в форме u(i), и характеристик элементов, управляемых напряжением, в форме i(u). Однозначность топологических уравнений, связанная с их линейной независимостью, достигается выделением дерева цепи и записи уравнений первого закона Кирхгофа для его главных сечений и уравнений второго закона для главных контуров. Если в составляемой системе целесообразно сохранить управляющие величины элементов с немонотонными характеристиками, то управляемые напряжением резисторы следует включить в дерево, ветви которого описываются напряжениями, а резисторы, управляемые током, — отнести к связям. В случаях, когда это условие выполнить не удается (в цепи существуют контуры из элементов, управляемых напряжением, и сечения из элементов, управляемых током), можно использовать следующий искусственный прием. Элемент с характеристикой, управляемой напряжением (рис. 28.1, а), представляется в виде последовательного соединения линейного резистора с сопротивлением R = u'/i и нелинейного резистора с характеристикой i(u") = i(u – Ri) (рис. 28.1, б). Это позволяет исключить контур из элементов, управляемых напряжением, так как введенный линейный резистор R может быть отнесен к связям.

Рис. 28.1

Аналогично выделением параллельной линейной проводимости из управляемого током резистора можно исключить сечение из элементов, управляемых током. В связи с этим будем далее рассматривать лишь цепи, в которых особые контуры и сечения отсутствуют.

Разумеется, линейность топологических уравнений дает широкие возможности исключения тех или иных токов и напряжений из системы уравнений цепи. Поэтому возможен и иной путь формирования уравнений системы, при котором управляемые напряжением элементы относят к связям, а их напряжения выражают через напряжения ветвей дерева с помощью уравнений второго закона Кирхгофа. Таким же образом при включении в дерево элементов, управляемых током, их токи будут исключены из решаемой системы при использовании уравнений первого закона, записанных для главных сечений дерева.

Громоздкость процедуры решения уравнений цепи существенно зависит от числа уравнений. Поэтому перед непосредственным решением следует использовать линейные уравнения системы для исключения возможно большего числа токов и напряжений.

Рассмотрим пример формирования уравнений цепи, включающей два линейных и три нелинейных резистора (рис. 28.2).

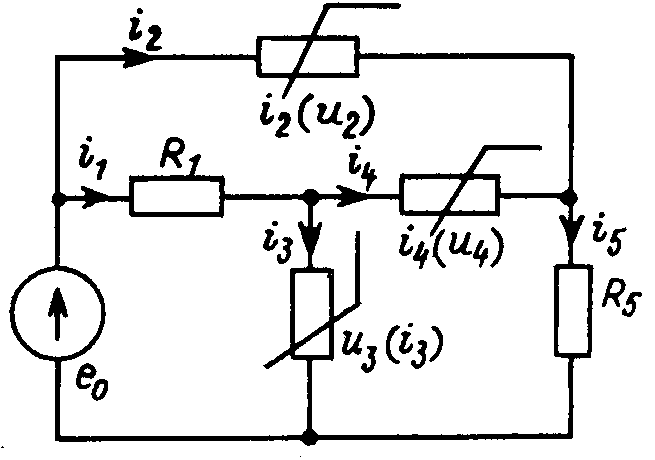
Рис. 28.2

Включим в дерево ветви, описываемые величинами e₀, u₂, u₄; к связям будут относиться ветви с токами i₁, i₃ и i₅. Уравнения для главных сечений имеют вид:

i₂ + i₁ = i₃ + i₅;  i₄ =  i₁- i₃.

Для главных контуров выбранного дерева запишем:

u₂ - u₄ = i₁R₁; e₀ = u₂ - u₄ + u₃; e₀ = u₂ + i₅R₅.

Полученная система содержит восемь неизвестных и вместе с выражениями характеристик элементов i₂(u₂), i₄(u₄), u₃(i₃) образует полную систему уравнений цепи. Число совместно решаемых уравнений можно сократить, исключив токи i₁ и i₅ и представив их в виде:

i₁ = (u₂ - u₄)/R₁;  i₅ = (e₀ - u₂)/R₅.

В результате получим систему, содержащую лишь управляющие величины u₂, u₄ и i₃:

i₂(u₂) +(u₂ - u₄)/R₁ = i₃ + (e₀ - u₂)/R₅;

i₄(u₄) = (u₂ - u₄)/R₁ -  i₃;

e₀ = u₂ - u₄ + u₃(i₃).

Поскольку ток i₃ допускает явное представление через другие величины

i₃ = (u₂ - u₄)/R₁ - i₄(u₄),

то и его можно исключить. В результате подстановки последнего выражения в остальные уравнения системы получим два нелинейных уравнения с неизвестными u₂ и u₄, которая имеет общий вид:

φ₁(u₂, u₄) = 0;  φ₂(u₂, u₄) = 0.