Тема 2. УЗЛОВЫЕ УРАВНЕНИЯ (задачи с решением)
Перейти к задачам без решения
|
Задача 2.1. На основе решения узловых уравнений (см. п. 3.1), рассчитать распределение напряжений и токов в цепи (рис. П2.1) при следующих значениях параметров:
Pис. П2.1 |
Примем за опорный — “ 0 ” один из узлов и пронумеруем все остальные узлы. Искомыми являются узловые напряжения — их напряжения u10, u20, u30 относительно опорного узла. Система трех узловых уравнений имеет следующий общий вид:
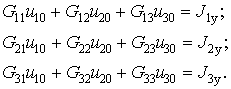
Для удобства будем оперировать проводимостями ветвей, которые равны обратным величинам их сопротивлений (Gk = 1/Rk). Имеем:
Собственные проводимости узлов Gkk — диагональные элементы матрицы узловых проводимостей — определяются как сумма проводимостей всех ветвей, подключенных к k-ому узлу:
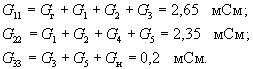
Общие проводимости узлов Gkn равны взятой с обратным знаком сумме проводимостей ветвей, соединяющих эти узлы:
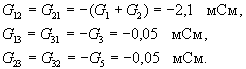
При определении узловых токов — правых частей системы узловых уравнений — будем считать сначала все источники независимыми. Узловой ток Jkу равен алгебраической сумме источников тока, действующих в ветвях, подключенных к k-му узлу. Источники ЭДС e, включенные последовательно с проводимостями G, учитываются произведениями eG. При этом источники, направленные к данному узлу, учитываются со знаком “плюс”, а противоположно направленные — со знаком “минус”:
Записанные выражения содержат неизвестные управляющие ток i2 и напряжение u5, которые необходимо выразить через узловые напряжения. Используя уравнения Кирхгофа для контуров, соединяющих узлы 0 ® 3 ® 2 ® 0 и 0 ® 1 ® 2 ® 0, найдем:
Разрешая последнее уравнение относительно i2 с использованием полученного выражения для u5, имеем:
Подставив эти соотношения в систему, перенося в левые части члены, содержащие неизвестные узловые уравнения и группируя члены, приведем ее к виду:
Решение этой системы дает: u10 = 0,828 В; u20 = 0,824 В; u30 = – 0,788 В.
По найденным узловым напряжениям токи в ветвях цепи найдем с помощью второго закона Кирхгофа:
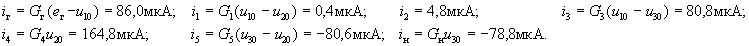
Проверку полученного решения можно осуществить с помощью первого закона Кирхгофа.
При работе в режиме изучения теоретического материала вернитесь назад к тексту Лекции 3.
|
Задача 2.2. Рассчитать распределение напряжений в цепи (рис. П2.2) с идеальным источником ЭДС e1 = 0,5 B (см. п. 3.6). Параметры элементов схемы равны: R1 = 50 кОм, R2 = 20 кОм, R3 = R4 = R5 = R6 = 0,5 кОм, R7 = 1 кОм.
Pис. П2.2 |
Примем за опорный — “ 0 ” один из узлов, к которому присоединен идеальный источник и пронумеруем все остальные узлы. При этом точку соединения последовательно включенных ветвей 4 целесообразно рассматривать как узел, поскольку в этом случае управляющее напряжение u источника e2 непосредственно выражается через узловые напряжения u = u10 – u40.
Уравнение для узла 1, к которому подключен идеальный источник ЭДС, не составляется, поскольку его узловое напряжение u10 задается этим источником u10 = e1 = 0,5 В. Используя правила формирования элементов матрицы узловых проводимостей, найдем:
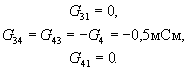
Узловые токи выражаются как
Перенося член, содержащий известную величину u10, в правую часть системы, а член с u40 — в левую, приведем систему к виду:
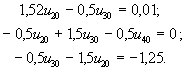
Решение системы имеет вид: u20 = 0,0985 В; u30 = 0,2796 В; u40 = 0,7401 В. Токи в резистивных ветвях равны:
Ток в ветви 2, параллельной идеальному источнику, не зависит от токораспределения в остальной части схемы. Токи в последовательно включенных ветвях 4 и 5, очевидно, равны друг другу.
При работе в режиме изучения теоретического материала вернитесь назад к тексту Лекции 3.
