Тема 22. СИНТЕЗ ПАССИВНЫХ ДВУХПОЛЮСНИКОВ
(задачи с решением)
Перейти к задачам без решения
|
Задача 22.1. Осуществить реализацию входного сопротивления
|
Это выражение представляет входное сопротивление цепи без потерь — степени полинома числителя нечетные, знаменатель имеет лишь четные степени. Нули
Z(s) (
;
) и полюсы (
;
) чередуются на мнимой оси.
Разложение Z(s) на сумму дробей
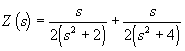ведет к первой канонической схеме — реализации в виде последовательного соединениях двух LC-контуров (рис. П22.1, а) с параметрами, указанными на рисунке.
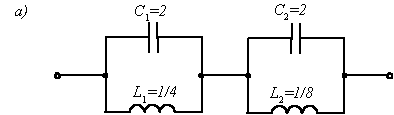
Рис. П22.1
Обратная величина 
является неправильной дробью, разложение ее на сумму дробей с выделением целой части дает
.
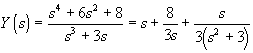Этому представлению отвечает реализация в виде параллельного соединения катушки
, емкости 
и последовательной LC-цепочки с 
и 
(рис. П22.1,б).
Поскольку проводимость Y(s) имеет полюс при s = ¥, то разложение в цепную дробь осуществляется для этого выражения. Деление, начиная со старших степеней, приводит к следующим результатам:
; 
; 
.
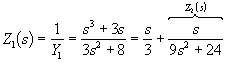Соответствующая схема изображена на рис. П22.1, в.
Наличие полюса Y(s) при s = 0 позволяет получить четвертую каноническую схему разложением Y(s) в цепную дробь. Однако теперь процесс деления выполняется, начиная с младших степеней s:
; 
; 
.
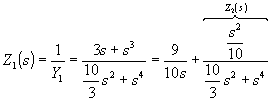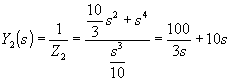Полученная схема изображена на рис. П22.1, г.
Отметим, что все канонические реализации
Z(s), изображенные на рис. П22.1, обладают идентичными свойствами — они имеют одинаковые значения
при любой частоте w. Так, при частотах, близких к нулю, когда можно пренебречь токами, протекающими через емкостные ветви, входное сопротивление всех четырех схем стремится к величине
, равной отношению младших степеней полиномов числителя и знаменателя. При
, когда, наоборот, можно пренебречь токами в индуктивных ветвях,
Z(s) стремится к величине 1/s, определяемой отношением старших степеней обоих полиномов. Эти результаты могут быть получены непосредственно по схемам, если при
все емкостные ветви считать разомкнутыми, а при
— разомкнуть ветви с индуктивностями.
|
Задача 22. 2. Реализовать цепь, входное сопротивление которой выражается функцией
|
Расположение двух нулей
Z(s) (
; 
) и полюсов (
), изображенное на рис. П22.2, а,
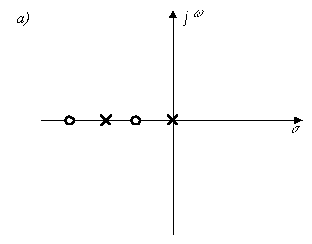
Рис. П22.2
показывает, что рассматриваемое выражение соответствует RС-цепи (нули и полюсы чередуются на вещественной оси, при s = 0 Z(s) имеет полюс). Поэтому при разложении на сумму простейших дробей будем рассматривать функции Z(s) и Y(s)/s:
; 
.
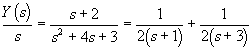Схемы реализации цепи, отвечающие этим двум выражениям, приведены на рис. П22.2, б, в.
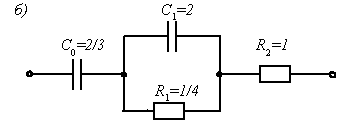
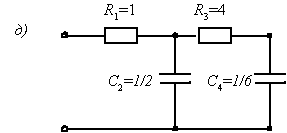
Рис. П22.2
Наличие полюса Z(s) при s = 0 позволяет осуществить разложение Z(s) на сумму простейших дробей в форме, основанной на делении, начиная с младших степеней:
; 
; 
.
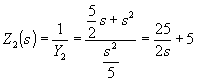Схемная реализация этого процесса приведена на рис. П22.2, г.
Второй вариант цепной реализации получим также из
Z(s). Поскольку значение 
, то такое разложение можно выполнить, начиная со старших степеней числителя и знаменателя:
; 
; 
.
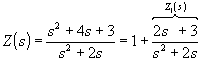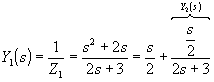Этому представлению Z(s) отвечает схема, изображенная на рис. П22.2, д.
|
Задача 22.3. Осуществить канонические реализации операторного сопротивления
|
Это выражение не имеет ни полюсов, ни нулей при
s = 0 и
. Его нули (
;
)
и полюсы (
; 
) отрицательны и чередуются на вещественной оси. Поскольку
, то искомая цепь относится к классу
RL, поэтому разложение на сумму простейших дробей осуществим для отношения
,
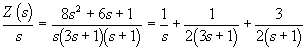откуда
.
Первая реализация представляет последовательное соединение резистора R0 и двух параллельных RL-контуров (рис. П22.3, а).
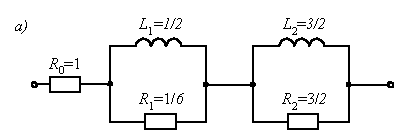
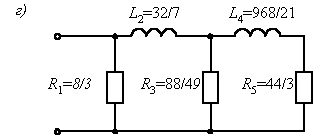
Рис. П22.3
Для получения второй канонической схемы разложим Y(s) = 1/Z(s) на сумму простейших дробей
.
Соответствующая реализация схемы представлена на рис. П22.3, б.
С учетом того, что Z(0) = 1 > 0, разложение выражения Z(s) в цепную дробь в данном случае можно осуществить, начиная деление полиномов числителя и знаменателя с младших степеней s (3-й вариант в табл. 24.1).
Схема последовательного деления имеет вид
; 
;
; 
.
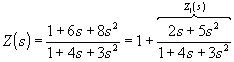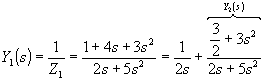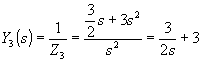В результате разложения получим схему, приведенную на рис. П22.3,в.
Четвертый канонический вариант реализации (рис. П22.3, г) получим, осуществляя разложение проводимости цепи
RL в цепную дробь, поскольку 
имеет конечное значение (4-й вариант в Табл. 24.1). Деление в этом случае производится, начиная со старших степеней полиномов:
; 
;
; 
.
|
Задача 22.4. Осуществить реализацию
передаточных функций |
Осуществим реализацию первой функции с помощью Г-образной схемы. Формулы для параметров ее ветвей позволяют получить следующие результаты:
; 
Положительность и вещественность Z1 и Z2 обеспечиваются, если в качестве Q(s) выбрать функцию Q(s) = as. При а =1 имеем:
; 
,
т. е. ветви Г-образного четырехполюсника представляют катушку и конденсатор.
Рассмотрим реализацию
второй передаточной функции 
. Она имеет постоянный модуль при s = jw
и нули в правой
полуплоскости. Поэтому ее реализация с
помощью минимально фазовой Г-образной цепи
невозможна.
При реализации с помощью симметричной мостовой схемы в режиме холостого хода использование соответствующих формул позволяет получить для сопротивлений плеч моста:
; 
.
В данном случае наиболее простой результат получим, принимая в качестве полинома знаменателя Q(s) = 2s. При этом Z1(s) = 2; Z2(s) = (2s2+4)/(2s) = s+2/s, и схема, реализующая передаточную функцию K(s), имеет вид, изображенный на рис. П.22.4, а.
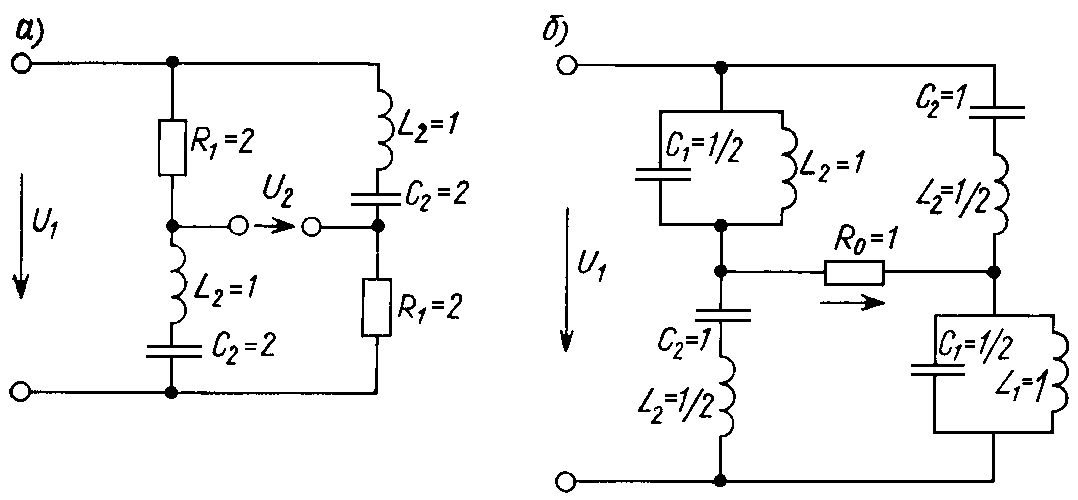
Рис. П.22.4
Если та же функция K(s) должна быть реализована в режиме согласованной нагрузки, то сопротивления плеч моста определим по формулам:
; 
.
из которых при R0 = 1 следует, что реализация осуществляется с помощью схемы, приведенной на рис. 24.11, б.
.
.
.
и