Как мы установили, идеальный фильтр нижних частот должен иметь частотные характеристики, изображенные на рис. 13.5, а его передаточная функция — описываться соотношениями:

Рис. 13.5

При подаче на вход такого фильтра сигнала f₁(t) со спектральной плотностью F₁(jw) на выходе будем иметь сигнал, Фурье-изображение которого равно F₂(jw) = K(jw)F₁(jw). Поэтому для выходного сигнала

Первый сомножитель подынтегральной функции отличен от нуля лишь при – w_c < w < w_c, и последний интеграл можно переписать в виде

При подаче на вход дельта-функции f₁(t) = d(t) (рис. 13.6, а), спектральная плотность которой равна F₁(jw) = 1, выходной сигнал выражается как

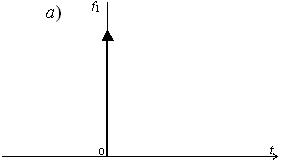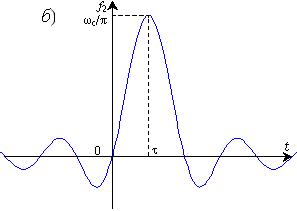Рис. 13.6

Таким образом, сигнал на выходе рассматриваемого идеального фильтра (рис. 13.6, б) должен был бы существовать и при t < 0, в то время как вызывающий его входной сигнал при t < 0 отсутствует. Иными словами, рассматриваемая идеальная цепь была бы способна вырабатывать выходной сигнал, прежде чем на ее вход подано вызывающее этот сигнал воздействие. Очевидно, никакая реальная физическая система подобным свойством, противоречащим принципу причинности, обладать не может. Отсюда следует, что построить фильтр с характеристиками, изображенными на рис. 13.5 — c постоянством передачи в полосе пропускания, нулевой передачей в полосе задерживания и скачкообразным переходом от одной полосы к другой  — принципиально невозможно. В связи с этим требования к амплитудно-частотной характеристике физически реализуемого фильтра, помимо сформулированных, должны включать также наличие полосы перехода — диапазона частот, разделяющего полосы пропускания и задерживания. В полосе перехода значения коэффициента передачи не нормируются, и происходит его плавное изменение от значений, требуемых в полосе пропускания до значений, допустимых в полосе задерживания.