Одна из простейших схем пассивного фильтра нижних частот, содержащая две индуктивности и емкость, приведена на рис. 13.7. Предположим, что нагрузкой фильтра нижних частот, представляющего  симметричный четырехполюсник с параметрами Z₁ = Z₃ =; Z₂ = , является его характеристическое сопротивление Z_н = Z_c. 

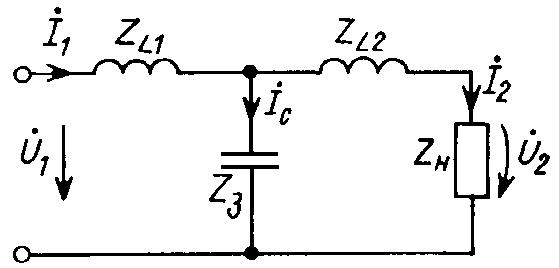
Рис. 13.7

Характеристические параметры такого четырехполюсника, определенные в п. 12.9, выражаются соотношениями:

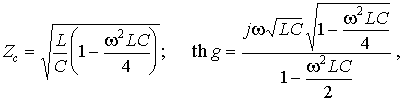
или в безразмерной форме, с введением безразмерной частоты ЦLC/2 = w_*:

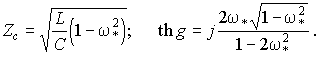
Из последнего соотношения, используя формулу п. 12.9, найдем

Из этого выражения видно, что при w_* < 1 или при w < w_c < 2/ЦLC мера передачи является чисто мнимой величиной. Это неравенство определяет полосу пропускания фильтра, в которой затухание a = 0.

Характеристическое сопротивление, вещественное в полосе пропускания, уменьшается от значения Z_c0 = ЦL/C при w = 0 до нуля на частоте среза w_c. Это не позволяет обеспечить настройку фильтра в режим согласования во всей полосе пропускания: при нагрузке на постоянное сопротивление условие согласования можно выполнить лишь для одной фиксированной частоты.

В полосе задерживания характеристическое сопротивление имеет индуктивный характер. При этом схема рис. 13.7 состоит из одних реактивных элементов, и фазовый сдвиг между входным и выходным напряжениями равен 180°.

В полосе пропускания коэффициент фазы b = 2 arcsin w_* и, следовательно, условие линейности фазочастотной характеристики фильтра не выполняется даже при согласованной нагрузке.

В полосе задерживания мера передачи имеет вещественную часть

.

Частотные зависимости a, b и Z_c изображены на рис. 13.8.

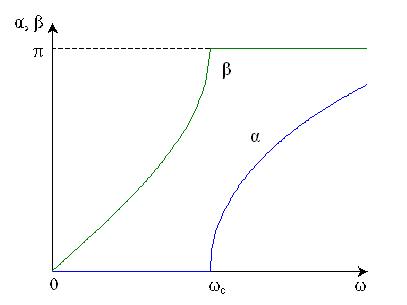
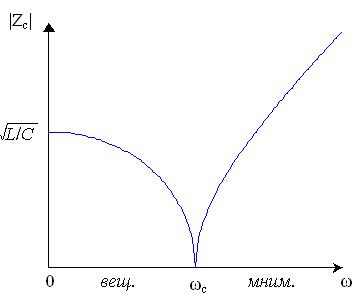
Рис. 13.8

Асимптотическое выражение для коэффициента затухания при w ® ¥ имеет вид a = 2 ln 2w, или в децибелах — 20 ´ 2 lg 2w = 20 lg 4 + 40 lg w — асимптота логарифмической АЧХ фильтра имеет наклон 40 дБ/дек. Для практических применений такой характер роста затухания зачастую является слишком медленным. Более резкое возрастание коэффициента затухания в полосе задерживания получим при каскадном включении нескольких Т-образных звеньев. Трехзвенный фильтр (рис. 13.9) имеет асимптотический наклон ЛАХ в области высоких частот — (3 ´ 40 = 120 дБ/дек). Однако и у него сохраняется невозможность согласования с резистивной нагрузкой в полосе пропускания.

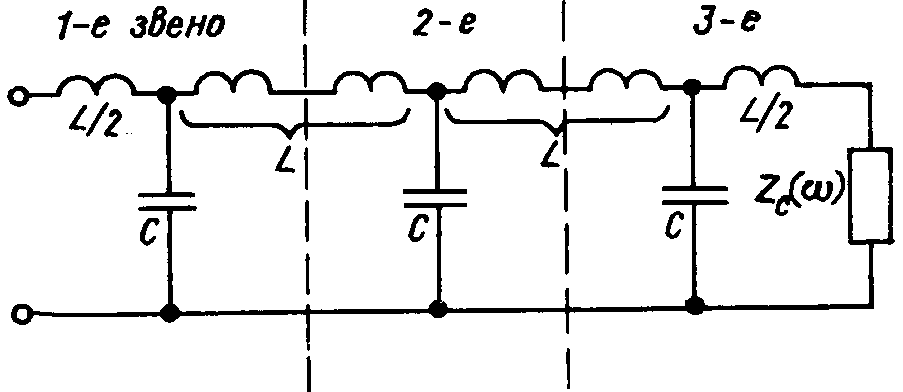
Рис. 13.9

При постоянстве нагрузочного сопротивления фильтра Z_н = R₀ = const условие a = 0 в полосе пропускания не может быть соблюдено. Покажем это на примере однозвенного фильтра с параметрами Z₁ = Z₃ = jwL/2; Z₂ = 1/jwC, нагруженного на сопротивление Z_н = R₀. Воспользуемся выражением коэффициента передачи нагруженного четырехполюсника (см. п. 12.6) K_U = = Z_н/(A₁₁Z_н + A₁₂).

Используя связи между A- и Z-параметрами (Приложение 1) и соотношения для параметров Т-образной схемы (п. 12.2), получим

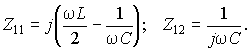Поэтому ; = = = .

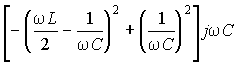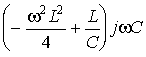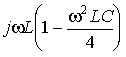Это дает для коэффициента передачи четырехполюсника, нагруженного на сопротивление R₀:

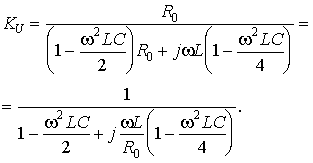
Приведем это выражение к безразмерным переменным, вновь принимая w_* = wЦLC:

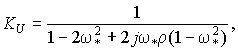
где r = ЦL/C /R₀.

Квадрат модуля знаменателя последнего выражения равен

Отсюда видно, что при любом постоянном значении r (или R₀) условие постоянства модуля коэффициента передачи фильтра в полосе пропускания обеспечить не удается.

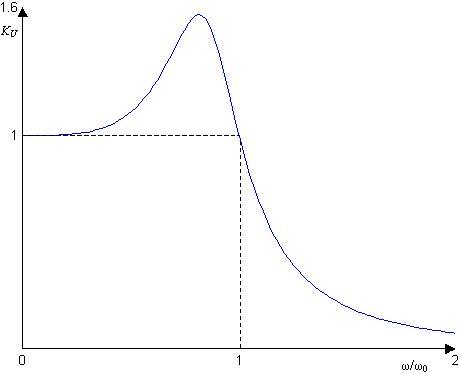
Рис. 13.10

Это иллюстрируется графиком рис.13.10 для r = 1 (или R₀ = ЦL/C), когда выражение модуля коэффициента передачи имеет вид

Таким образом, при формулировке реалистичных требований к частотным характеристикам фильтров (нагруженных на постоянное сопротивление, не зависящее от частоты) необходимо допустить изменения модуля коэффициента передачи фильтра в полосе пропускания (ПП) (w_с1 < w < w_c2), не превышающие некоторого значения DK (рис. 13.11, а), задаваемого в качестве исходного при расчете фильтра, и плавный переход к полосе задерживания (ПЗ) (w < w_з1, w > w_з2), где значения коэффициента передачи не должны превышать некоторого заданного значения K_max.

a)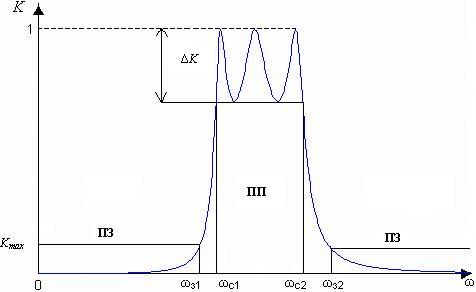

б)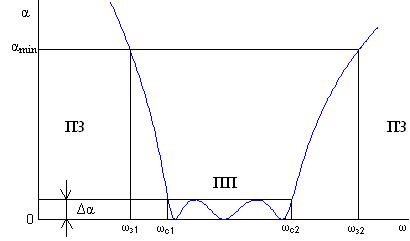

Рис. 13.11

Обычно эти характеристики задаются в децибелах — допустимая неравномерность коэффициента передачи в полосе пропускания характеризуется максимальным значением ослабления сигнала в полосе пропускания. Поскольку a = 20 lg U₁/U₂ = – 20 lg K_U, то Da = – 20 lg (1 – DK). Аналогично, ослабление выходного сигнала в полосе задерживания не должно быть ниже a_min = – 20 lg K_max (рис. 13.11, б).