Поскольку передаточная функция K(jw) любой электрической цепи с постоянными сосредоточенными параметрами — дробно-рациональная функция аргумента jw, то выражение квадрата ее модуля K² также будет дробно-рациональной функцией аргумента w². Задача аппроксимации частотной характеристики фильтра нижних частот состоит в выборе такого вида этой функции, которая наиболее близка к характеристике идеального фильтра НЧ (см. рис. 13.2, а).

Обозначим искомую аппроксимирующую функцию H²(w). Перейдем к безразмерной частоте, принимая за базисную частоту среза фильтра w_c. Опуская индексы, обозначим безразмерную частоту w. Задача аппроксимации АЧХ фильтра нижних частот сводится к поиску такой рациональной дроби H²(w), у которой при 0 < w < 1 отклонения от единицы не превосходят заданного малого значения, а при w > 1 значение H²(w) резко уменьшается с ростом частоты. Поставленным условиям удовлетворяет дробь вида H²(w) = 1/[1 + e²Q²_n(w)], где Q_n(w) — полином степени n, модуль которого в промежутке 0 < w < 1 не превосходит единицы, монотонно возрастающий при w > 1; e — число, определяющее неравномерность характеристики в полосе пропускания. При нормировке соответствующего полинома с Q_n max _max = 1 в полосе пропускания функция H заключена в пределах 1/Ц1 + e² £ H £ 1. Поэтому величина e связана с характеристикой неравномерности передачи фильтра в полосе пропускания Da. Так как Da = – 20 lg(1/Ц1 + e²) = 10 lg (1 + e²), то соотношение, выражающее обратную зависимость, имеет вид e = . Например, для заданной неравномерности в 3 дБ минимальное значение H_min в полосе пропускания равно 1/Ц2. Ему соответствует e  = 1.

В полосе задерживания значение H(w) уменьшается тем быстрее, чем выше показатель степени полинома n. Заданная величина минимального ослабления в полосе задерживания a_min выражается через введенные функции: a_min = – 20 lg H(w_з) = 10 lg [1 + w²Q²_n(w_з)], где w_з — граничная частота полосы пропускания. При заданных a_min, e, w_з и семействе функций Q_n из последней связи можно определить степень n, обеспечивающую требуемый спад характеристики H(w) в полосе задерживания.

Один из наиболее простых способов решения задачи аппроксимации состоит в выборе в качестве Q_n(w) степенной функции wⁿ. При этом выражение квадрата модуля H² принимает вид H² = 1/(1 + e²w²ⁿ). Эти зависимости монотонны во всем частотном диапазоне. Из рис. 13.12, на котором изображены кривые H²(w) при n от 1 до 4, следует, что с ростом n  в полосе задерживания — при w > 1 — значения H² уменьшаются, а  начальная часть кривых становится все более плоской — они приближаются к характеристике идеального ФНЧ. Рассматриваемый класс аппроксимации определяет фильтры с максимально плоскими характеристиками (фильтры Баттерворта).

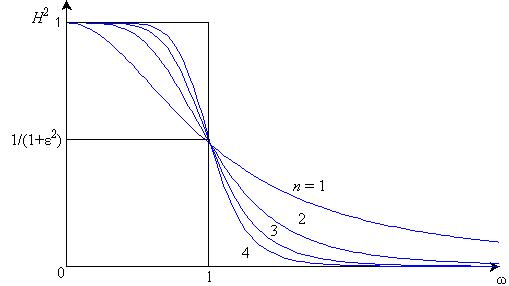
Рис. 13.12

Другой подход связан с использованием в качестве полиномов Q_n(w) полиномов Чебышева T_n(w) = cos(n arccos w). Известно, что из всех полиномов n-й степени с одинаковыми старшими коэффициентами полином Чебышева наименее уклоняется от нуля на отрезке (– 1, 1), где он попеременно принимает максимальные и минимальные значения ± 1. Такое свойство полиномов Чебышева определяет равноколебательный характер функции

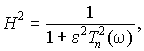
которая в полосе пропускания колеблется между значениями 1/(1 + e²) и единицей. Число экстремумов функции в полосе пропускания  H² равно степени полинома n. С увеличением n спад частотной характеристики в полосе задерживания становится более резким, и характеристики этого класса также приближаются к характеристике идеального фильтра нижних частот (рис. 13.13).  Подобная аппроксимация носит название равноколебательной, а соответствующие фильтры называются фильтрами Чебышева.

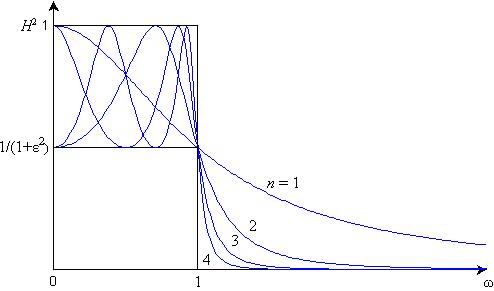
Рис. 13.13

Сопоставим максимально плоские и равноколебательные характеристики, отвечающие одним и тем же значениям n и e. При n = 3 и e = 1  = 1/(1 + w⁶), а  = 1/[1 + (4w³ – 3w)²]. В полосе задерживания (w > 1) вторая зависимость убывает быстрее. Например, при w = 2 H_{м. п} = 0,124, а H_р.к = 0,038. Это соотношение носит общий характер: в полосе задерживания при данном n и любой частоте H_р.к < H_{м. п}.  Поскольку степень полинома n определяет число реактивных элементов в схеме фильтра, то заданное ослабление в полосе задерживания обеспечивается при равноколебательной аппроксимации более простой схемой с меньшим числом элементов, чем при максимально плоской.