18.1. РЕШЕНИЕ УРАВНЕНИЙ СОСТОЯНИЯ ЧИСЛЕННЫМИ МЕТОДАМИ
Для использования стандартных методов численного интегрирования обыкновенных дифференциальных уравнений интегрируемая система должна быть записана в нормальной форме
![]() ,
, ![]() .
.
Здесь принята общая запись правой части уравнений состояния, охватывающая и нелинейные уравнения, так как рассматриваемые ниже методы пошагового интегрирования одинаковы для линейных и нелинейных уравнений. Именно к такой форме приводит метод переменных состояния. Его применение целесообразно и при формировании уравнений для численного интегрирования.
Основой используемых численных методов является вычисление приращений переменных состояния Dxj за рассматриваемый промежуток времени — шаг интегрирования Dtk = tk + 1 – tk = h
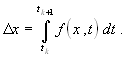
В последнем выражении индексы j у переменных x и f для упрощения записи опущены.
Методы численного интегрирования, известные из курса численного анализа, различаются по способу аппроксимации подынтегральной функции в последнем выражении. Наиболее простой вид имеют формулы
Поскольку и последнее выражение содержит значения fk+1, не известные в начале вычислений на данном шаге, то метод трапеций также является неявным.
Реализация неявных методов требует на каждом шаге решения системы уравнений относительно неизвестных значений xk+1 в конце данного шага. Выбор шага интегрирования h связан с обеспечением точности и устойчивости численного решения. Обеспечение устойчивости является определяющим при интегрировании так называемых жестких систем дифференциальных уравнений, у которых корни характеристического уравнения резко различаются по модулю.
Пример расчета переходного процесса в цепи, рассмотренной в Задаче 14.1 путем численного интегрирования уравнений состояния рассмотрен в Задаче 14.3. Как следует из полученного решения, при принятом шаге интегрирования h = 10-5 с все три использованные метода обеспечивают достаточно высокую точность решения. В то же время при попытке увеличить шаг интегрирования до значения h = 8·10-4 с явный метод Эйлера теряет устойчивость, неявные же методы дают устойчивые результаты, хотя их точность ухудшается. В условиях рассмотренной задачи вопрос выбора подходящего метода интегрирования несущественен, так как точный результат обеспечивает любой из сопоставляемых методов за приемлемое число шагов, т.е. при разумных затратах машинного времени. Однако это имеет место не всегда. Так, при уменьшении индуктивности в рассматриваемой схеме (рис. П14.1) до значения L = 10-4 Гн предельный шаг интегрирования, выбираемый по условию устойчивости в явном методе Эйлера сокращается до значения hм = 8·10-7 с. Поскольку общая длительность переходного процесса при таком уменьшении индуктивности сохраняется практически неизменной, то теперь для получения полной картины переходного процесса явным методом необходимо совершить 0,01/ hм @ 12500 шагов. Очевидно, что для еще меньших значений индуктивности L в рассматриваемой задаче (что ведет к увеличению жесткости интегрируемой системы уравнений) подобное соотношение будет еще более невыгодным. Это характерно для решения жестких систем дифференциальных уравнений любым явным методом численного интегрирования.