Описание связей между изображениями по Лапласу входных U₁(s), I₁(s) и выходных U₂(s), I₂(s) величин операторными соотношениями привело нас к наиболее общей форме представления входных и передаточных функций в линейных электрических цепях:

; ; ; .

Функции Z(s), Y(s), K(s) — функции цепи — обладают рядом общих свойств. Изучение этих свойств необходимо, в частности, при решении задач синтеза цепей: определении структуры и параметров ее элементов по заданным входным и выходным токам и напряжениям. Это необходимо, например, при проектировании систем автоматики и связи, в которых нужно обеспечить заданный характер преобразования сигнала. Типичной в этом отношении является задача синтеза частотного фильтра. В дальнейшем будем использовать для входных и передаточных функций общее обозначение F(s), рассматривая эту величниу как функцию комплексного аргумента s = s + jw.

Вещественность. Параметры элементов цепи R, L, C входят в алгебраические уравнения, составленные для операторных изображений токов и напряжений на базе законов Кирхгофа, контурных или узловых уравнений, в комбинациях R, sL, 1/sC или 1/R, 1/sL, sC. Поэтому любая функция цепи, определяемая отношением изображений двух токов или напряжений, выражается рациональной дробью аргумента s:

.

Полином в знаменателе F(s) представляет характеристическое уравнение цепи. Он представляет собой главный определитель системы узловых или контурных уравнений D_Y или D_Z, в зависимости от того, какой из этих методов используют для описания цепи. 

Коэффициенты полиномов числителя b_k и знаменателя a_k дроби F(s), образованные произведениями сопротивлений, емкостей или индуктивностей элементов цепи, вещественны. Эти полиномы также можно представить в факторизованной форме

,

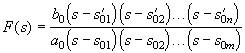(22.1)

где — корни числителя — нули F(s); s_0k — корни знаменателя — полюсы F (s).

Так как коэффициенты a_k и b_k являются вещественными, то при вещественных значениях оператора s функция цепи F(s) принимает вещественные значения

при .

(22.2)

Отсюда, в частности, следует, что комплексные нули s'_0k также, как и полюсы s_0k, — комплексно сопряженные.

Расположение полюсов и нулей. Полюсы функции F(s) s_0k — корни характеристического уравнения — определяют показатели экспонент, представляющих выходную величину при переходном процессе в цепи. В пассивной цепи корни s_0k могут лежать только в левой полуплоскости, причем на мнимой оси могут находиться лишь простые корни.

Нули входной функции также располагаются в левой полуплоскости: нули Z(s) — корни уравнения Z(s) = 0 — определяют показатели экспонент свободных составляющих переходного процесса при подаче на вход цепи напряжения от источника ЭДС е (рис. 22.1, а). Точно также нули Y(s) описывают составляющие переходного процесса, обусловленного подачей на вход сигнала от источника тока J₀ (рис. 22.1, б). Так как токи и напряжения в обоих переходных процессах со временем не могут неограниченно нарастать, то у входной функции корни как числителя, так и знаменателя должны находиться в левой полуплоскости.

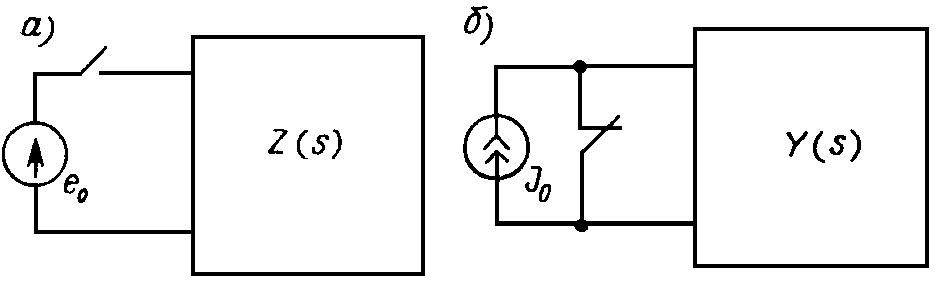
Рис. 22.1

С другой стороны, нули передаточной функции s'_0k не связаны подобным образом с реакцией цепи на возбуждение того или иного вида. Они определяют “комплексные частоты”, при которых сигнал на выходе цепи отсутствует и могут находиться также и в правой полуплоскости. Покажем это на примере простейшей симметричной мостовой RС-цепи (рис. 22.2, а).

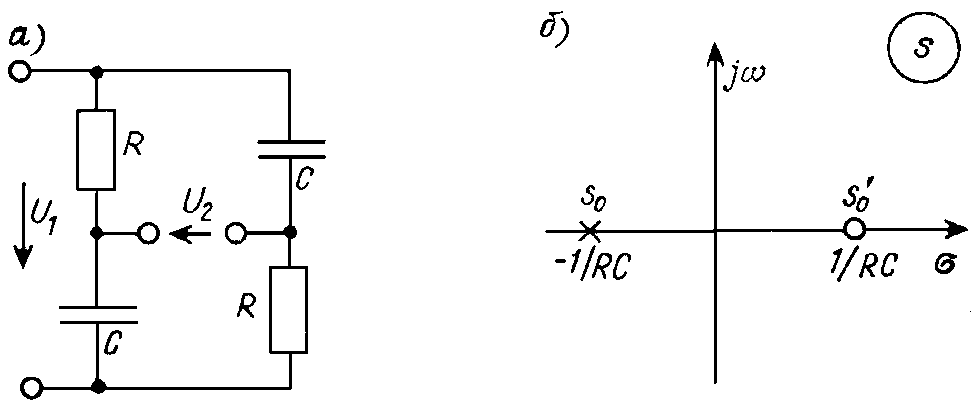
Рис. 22.2

Ее выходное напряжение U₂ — это разность падений напряжения на резисторе и конденсаторе . Учитывая, что токи I(s) в обеих параллельных ветвях одинаковы и равны I(s) = U₁(s)/(R + 1/sC), для передаточной функции получим

,

т. е. она имеет симметрично расположенные нуль s'₀ = 1/RC в правой и полюс s₀ = – 1/RC в левой полуплоскости (рис. 22.2, б). Наличие нулей в правой полуплоскости характерно для передаточных функций мостовых цепей. Их выходное напряжение определяется как разность падений напряжения на плечах моста, и коэффициенты b_k полинома числителя K(s) имеют различные знаки, что является признаком наличия нулей в правой полуплоскости.

Изображение полюсов и нулей функции цепи F(s) на комплексной плоскости позволяет наглядно проследить за характером частотных зависимостей модуля и аргумента комплексной функции F(jw) — ее амплитудно- и фазочастотной характеристиками —  во всем частотном диапазоне w (от нуля до бесконечности). Отдельные сомножители полиномов числителя и знаменателя F(s) (22.1) (s – s_0k) и (s – s'_0k) при s = jw изображаются на комплексной плоскости векторами, направленными из точек расположения полюсов и нулей в точку мнимой оси, соответствующую данной частоте w (рис. 22.3).

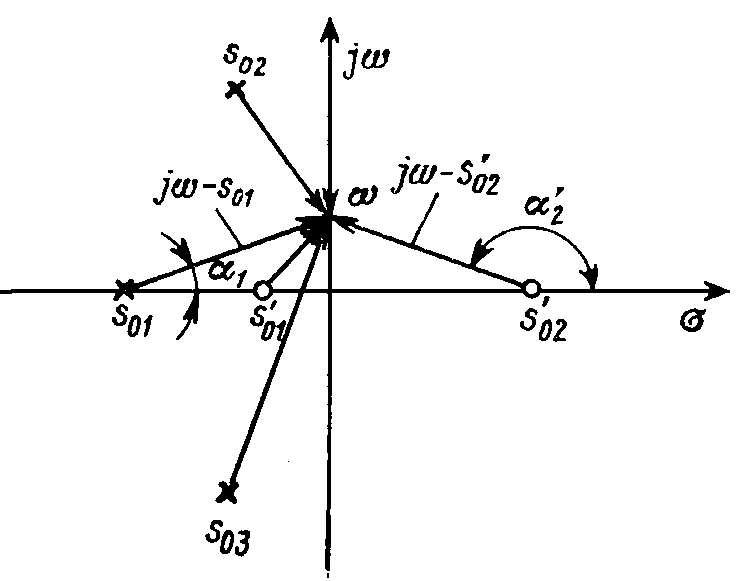
Рис. 22.3

Модуль функции F(jw) представляется отношением произведения модулей векторов jw – s'_0k, отвечающих нулям функции F(s), к произведению модулей векторов jw – s_0k, соответствующих ее полюсам. Аргумент F(jw) аналогично определяется разностью суммы аргументов a'_k векторов jw – s'_0k и суммы аргументов a_k векторов jw – s_0k (см. рис. 22.3).

Так, вещественным полюсам и нулям с ростом частоты соответствует монотонное увеличение модулей отдельных сомножителей  jw – s_0k и монотонное увеличение аргумента от 0 при w = 0 до p /2 при w = ¥. Для комплексного полюса или нуля s_0k = d_0k + jw_0k изменение модуля сомножителя имеет немонотонный характер — в точке оси w = w_0k, ближайшей к данной особой точке, модуль принимает минимальное значение, равное ½d_0k½. Это определяет заметные изменения модуля и фазы вблизи соответствующего полюса и нуля. Чем ближе полюс или нуль к мнимой оси, тем резче выражены изменения амплитудно- и фазочастотной характеристики в его окрестности.

Передаточные функции цепей с симметричным относительно мнимой оси расположением всех нулей и полюсов (например, рис. 22.2, б) имеют постоянный модуль при всех значениях w.

Рассмотрим два четырехполюсника, изображенных на рис. 22.4, а,б.

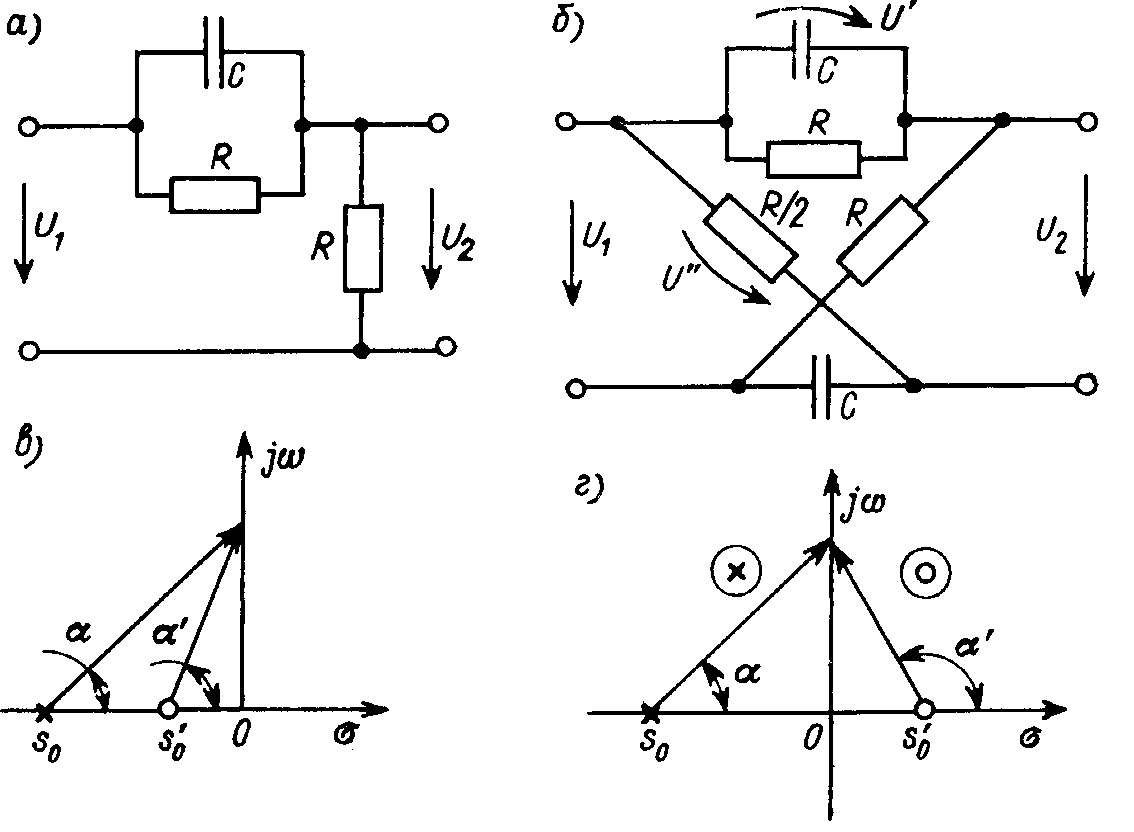
Рис. 22.4

Первый представляет собой делитель напряжения, в плечах которого включены сопротивления и Z₂ = R. Поэтому его передаточная функция равна

.

Передаточную функцию по напряжению второго четырехполюсника найдем как разность падений напряжения на плечах моста, каждая из параллельных ветвей которого также является делителем напряжения U₁:

.

Сопоставляя характер расположения полюсов и нулей двух цепей (рис. 22.4, в,г), приходим к выводу, что при одинаковых амплитудно-частотных характеристиках они обладают различными фазочастотными характеристиками. Поскольку аргумент числителя при s = jw у первого четырехполюсника меньше, чем у второго, то фазовый сдвиг q = a' – a между выходным и входным напряжениями у него меньше. Очевидно, еще сколь угодно много цепей, имеют такую же амплитудно-частотную характеристику, как и рассматриваемые две: добавление любого числа пар полюс - нуль, расположенных симметрично относительно мнимой оси, подобных обведенным кружками на рис. 22.4, г, не повлияет на вид амплитудной характеристики цепи. Из этого множества цепей первая из рассмотренных (рис. 22.4, а) дает минимальный фазовый сдвиг между выходным и входным напряжениями. Это связано с тем, что она не имеет нулей в правой полуплоскости. Такие цепи называются минимально-фазовыми. Для них характерна однозначная взаимозависимость между АЧХ и ФЧХ. Задание одной из этих характеристик позволяет однозначно восстановить другую. 

Для неминимально-фазовых цепей, передаточные функции которых имеют нули в правой полуплоскости, однозначная взаимосвязь между обеими частотными характеристиками отсутствует. Это свойство позволяет использовать неминимально-фазовые четырехполюсники для коррекции фазочастотных характеристик каскадно включенных с ними звеньев без изменения их амплитудно-частотных характеристик. Одна из возможных схем такого корректора — симметричная мостовая (скрещенная) цепь, в двух плечах которой помещены одинаковые активные сопротивления, а в двух противоположных плечах — одинаковые чисто реактивные сопротивления Z_LC, состоящие из произвольно соединенных элементов L, С (рис. 22.5, а).

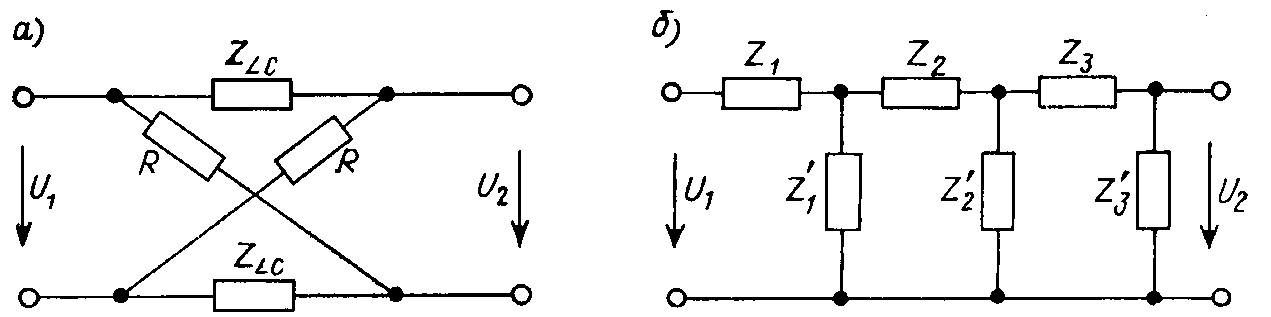
Рис. 22.5

Минимально-фазовым четырехполюсником, наоборот, является лестничная цепь (рис. 22.5, б), в которой продольные Z_k и поперечные Z'_k элементы представляют произвольные двухполюсники. Нули ее передаточной функции определяются значениями s, при которых либо сопротивления продольных ветвей равны бесконечности Z_k(s) = ¥, либо обращаются в нуль сопротивления поперечных ветвей — Z_k'(s) = 0. Эти условия связаны с полюсами и нулями сопротивлений двухполюсников и поэтому нули передаточной функции лестничной цепи s'_0k лежат только в левой полуплоскости. Таким образом, любая лестничная цепь является минимально фазовой.

Как следует из выражения (22.1), функция цепи F(s) полностью определена расположением ее нулей и полюсов на плоскости s и значением модуля при одной из значений s или  jw.

Пример исследования свойств цепи по расположению ее полюсов и нулей приведен в Задаче 20.1.