5.1. ОБЩИЕ ПОЛОЖЕНИЯ МЕТОДА СИГНАЛЬНЫХ ГРАФОВ

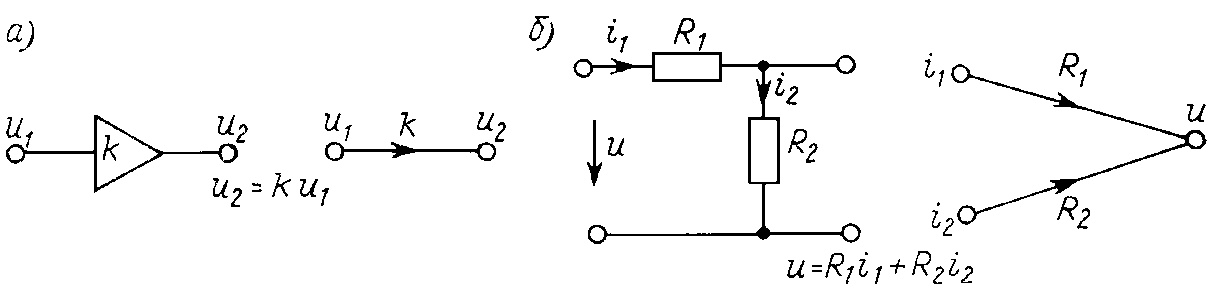
Наряду с алгебраическими уравнениями (Кирхгофа, узловыми или контурными) при исследовании цепей применяют эквивалентную им графическую форму изображения связей между переменными (токами и напряжениями) — сигнальный граф цепи, который строят из двух типов элементов — точек, называемых узлами, и соединяющих их линий со стрелками — ветвей графа. Узлам отвечают переменные (токи, напряжения и ЭДС), ветвям — количественные соотношения между ними. Каждой ветви сигнального графа приписывают коэффициент передачи (передачу) — множитель, указывающий величину, на которую умножается переменная, передаваемая по ветви от одного узла к другому в направлении стрелки. Связи между переменными выражены в форме x₂ = t₁₂x₁, где x_1,2  — напряжение, ток или ЭДС, а t₁₂ — сопротивление R, проводимость G или безразмерный коэффициент k. Сигнал, отвечающий узлу, к которому подходит несколько стрелок, равен сумме входящих в узел сигналов, умноженных на коэффициенты передачи соответствующих ветвей. Связь между входным и входным напряжениями усилителя u₁ и u₂ показана на рис. 5.1, а.

Рис. 5.1

Связь напряжения u на участке цепи, включающем два сопротивления R₁ и R₂, с токами i₁ и i₂ — на рис. 5.1, б.

Заданным при расчете сигналам (ЭДС и токам независимых источников) соответствуют истоки — узлы графа, не имеющие входящих ветвей.

Совокупность ветвей, проходящих через несколько узлов в направлении стрелок, — это путь графа. Ни один из узлов при этом не проходится дважды. Замкнутый путь называют контуром; контур из одной ветви называется петлей.

Сигнальный граф, изображающий все уравнения цепи, позволяет рассчитать все включенные в него переменные, причем расчет можно выполнить не чисто алгебраическими средствами, а с использованием введенных выше понятий путей и контуров. Однако в основе этих действий лежат те же алгебраические преобразования, которые трактуются как операции над элементами графа.

Сигнальный граф составляют на основе независимой системы соотношений между искомыми сигналами и заданными величинами — либо уравнений Кирхгофа и компонентных уравнений, либо узловых или контурных уравнений. Для построения графа система уравнений должна быть разрешена относительно искомых переменных.

Для схемы рис. 5.2, а, можно записать на основе законов Кирхгофа:

Изобразим на графе пять искомых величин: токи во всех ветвях с сопротивлениями и напряжения u₁ и u₂₃.

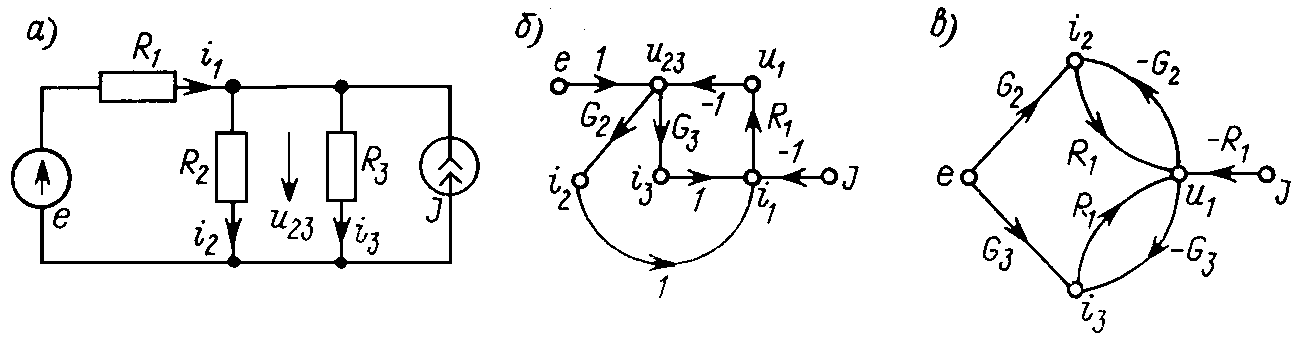
Рис. 5.2

Этим переменным отвечает преобразованная система:

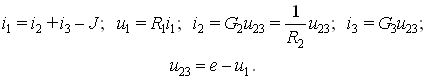
Узлы, соответствующие отдельным переменным, можно разместить произвольно на графе, однако лучше располагать ближе друг к другу те, что связаны уравнениями системы. Ветви графа отвечают отдельным слагаемым правых частей уравнений (рис. 5.2, б). Согласно первому уравнению, в узел i₁ входят три ветви. Передачи ветвей, соединяющих узлы i₂ и i₃ с узлом i₁, равны единице, ветвь J ®  i₁ имеет передачу (-1). Аналогично на графе изображают и остальные уравнения системы.

Поскольку граф с более простой структурой проще рассчитывать, то надо стремиться к тому, чтобы возможно большая часть переменных, не представляющих непосредственного интереса при расчете, была исключена на стадии формирования графа. Для этого, в частности, можно выбрать такую систему переменных, чтобы каждый двухполюсный элемент цепи описывался только одной переменной — током или напряжением. Подобный сигнальный граф называют компактным.