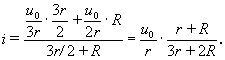6.5. ВЛИЯНИЕ ИЗМЕНЕНИЯ ПАРАМЕТРОВ НА РЕЖИМ В ЦЕПИ

Замена любого двухполюсного фрагмента цепи эквивалентным источником позволяет проследить за влиянием сопротивления участка цепи на протекающий по нему ток и напряжение на нем. При замене двухполюсника A (рис. 6.10, а) эквивалентным источником для его тока i и напряжения u имеем:

где e₀, i₀, R₀ — параметры эквивалентного источника.

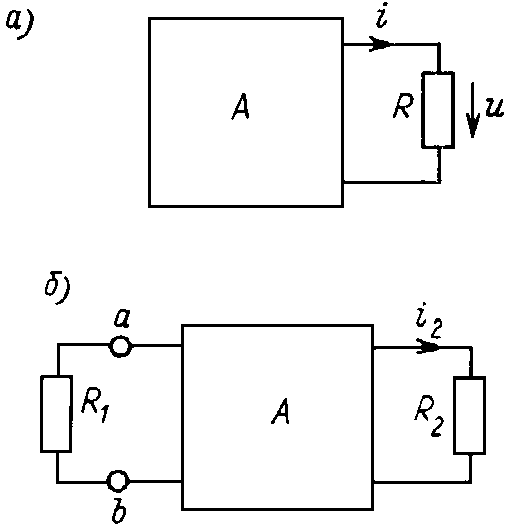
Рис. 6.10

Зависимость тока в некоторой ветви цепи i₂ (рис. 6.10, б) от сопротивления другой ветви R₁  можно определить в результате алгебраических преобразований цепи, поэтому по структуре искомая зависимость i₂(R₁) имеет вид рациональной дроби. Знаменатель ее формируется из главного определителя системы контурных уравнений, и следовательно, его можно записать, как и в рассмотренном выше случае, в форме R₁₀ + R₁, где R₁₀ — входное сопротивление цепи относительно зажимов ab сопротивления R₁. Для записи числителя рассмотрим режимы в цепи при R₁ = ¥  — размыкание ветви с R₁, и R₁ = 0 — короткое замыкание этой ветви. Обозначим токи i₂ в обоих режимах соответственно i₂₀ и i_2к. В режиме короткого замыкания, когда знаменатель искомого выражения становится равным R₁₀, в числителе дроби i₂(R₁) будем иметь член i_2кR₁₀. Если же R₁ ® ¥, то числитель стремится к выражению i₂₀R₁. Суммируя оба слагаемых, получим искомую зависимость:

В связи с этим зависимость тока, а также и напряжения в некоторой ветви от сопротивления другой ветви выражается дробно-линейной функцией. При положительных значениях R₁₀ и R₁ она имеет монотонный характер, однако в зависимости от соотношения между величинами i₂₀ и i_2к она может либо возрастать (при i_2к < i₂₀), либо убывать (при i_2к > i₂₀). Поэтому увеличение сопротивления в одной ветви цепи может приводить к увеличению тока в некоторых ветвях и к его уменьшению в других.

Таким образом, для определения зависимости тока в i₂ цепи от сопротивления другой ветви R₁ необходимо проанализировать три режима — найти искомый ток i₂ при разомкнутой ветви 1 с варьируемым сопротивлением i₂₀, при ее коротком замыкании i_2к и вычислить входное сопротивление цепи относительно зажимов варьируемого сопротивления R₁₀.

Полученные зависимости показывают, что входные и передаточные сопротивления и коэффициенты передачи любой цепи выражаются через ее параметры рациональными дробями, числители и знаменатели которых линейно зависят от сопротивлений любого элемента цепи R_k.  Поэтому алгебраические выражения входных и передаточных функций не могут содержать членов вида R_k², R_k³ и т.д. Подобные нелинейные члены могут появиться при промежуточных преобразованиях уравнений цепи, но они обязательно сокращаются и не входят в окончательные выражения.

Принцип дуальности позволяет установить аналогичные свойства входных и передаточных величин, выражаемых через проводимости элементов.

Пример. В цепи, включающей три резистора с одинаковыми сопротивлениями r (рис. 6.11) требуется определить зависимость тока i от сопротивления R.

Рис. 6.11

Найдем сначала входное сопротивление цепи относительно зажимов ab. При закороченном входном источнике имеем R_вх ab = 3r/2. При коротком замыкании R искомый ток определяем по формуле i_к = u₀/3r; при разомкнутой ветви i = u₀/2r. Подставляя найденные значения в общее выражение, получим