16.1. УРАВНЕНИЯ СОСТОЯНИЯ ПРОИЗВОЛЬНОЙ ЦЕПИ
Расчет переходного процесса в сложной цепи с любым числом конденсаторов и катушек можно выполнить на основе интегрирования уравнений состояния — дифференциальных уравнений, составленных относительно переменных состояния — токов катушек iL и напряжений на конденсаторах uC. Совокупность переменных состояния определяет единственным образом все остальные токи и напряжения цепи. Однако в цепи с произвольной конфигурацией токи катушек и напряжения на конденсаторах не всегда независимы. Так, например, напряжения на элементах контуров, состоящих из только из конденсаторов и источников ЭДС (Ce-контура) связаны уравнением второго закона Кирхгофа и, следовательно, не являются независимыми. То же имеем для сечений, состоящих из индуктивностей и источников тока (LJ-сечений), токи которых входят в уравнение первого закона Кирхгофа. При отсутствии в цепи таких особенностей все переменные состояния независимы, и порядок дифференциального уравнения, к решению которого сводится задача расчета переходного процесса, определяется общим числом n динамических элементов — катушек и конденсаторов цепи. Обозначим совокупность переменных состояния цепи, включающей p катушек и k конденсаторов, символами
![]()
Если цепь включает LJ-сечения, то каждое такое сечение снижает число независимых переменных на единицу. Также и каждый Ce-контур соответственно уменьшает число переменных. Поэтому в цепи с такими особыми сечениями и контурами общее число независимых переменных состояния, однозначно выражающих все остальные напряжения и токи, равно n – nJ – ne, где nJ — общее число LJ-сечений цепи; ne — число Ce-контуров. При выборе переменных состояния в подобных цепях из их числа исключают один из токов индуктивностей, входящих в каждое LJ-сечение и одно из напряжений uC, входящих в каждый Ce-контур.
В качестве совокупности переменных состояния данной цепи можно использовать не только указанный набор iL и uC, но и любую их линейную комбинацию, в частности, потокосцепления индуктивно связанных катушек и заряды конденсаторов, образующих сечение цепи. Такой выбор может упростить как формирование уравнений состояния, так и процедуру их решения.
Общий путь расчета переходного процесса методом переменных состояния основан на составлении n дифференциальных уравнений первого порядка относительно переменных состояния xj, записанных в нормальной форме Коши. Основой их для формирования служат уравнения Кирхгофа и компонентные уравнения элементов цепи, поэтому такая система уравнений состояния является линейной и может быть представлена в общей форме
![]() ,
, ![]()
Коэффициенты в правых частях уравнений состояния ajk определяются структурой цепи и параметрами ее элементов, функции fj(t) учитывают вклад внешних источников ЭДС и тока.
Систему n уравнений состояния можно свести известными математическими приемами к одному дифференциальному уравнению n-го порядка относительно одной из переменных состояния, подобно тому, как это было сделано выше при анализе переходных процессов в колебательном контуре (см. п.15.5 и п.15.6). Однако такое преобразование не является необходимым для последующего решения.
Систему уравнений состояния можно записать в общей матричной форме
![]() ,
,
где x — вектор переменных состояния; A — квадратная матрица; F(t) — вектор входных воздействий:
 ;
;  ;
; 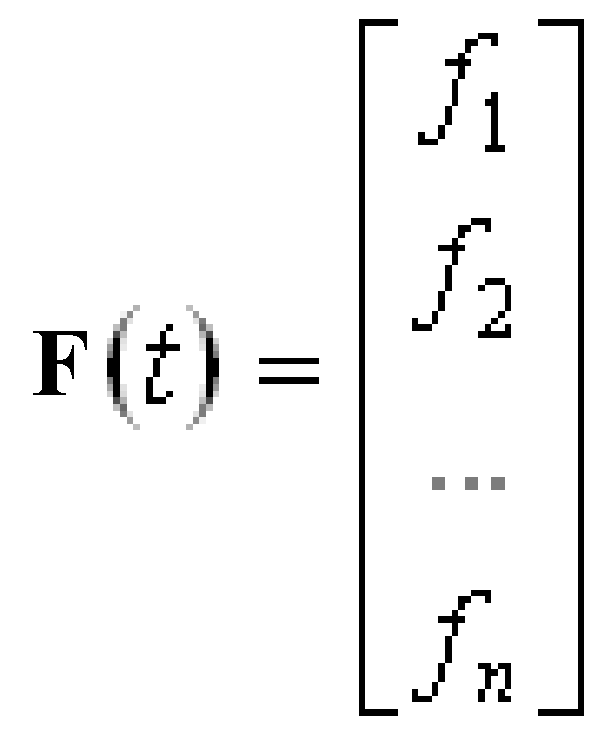 .
.