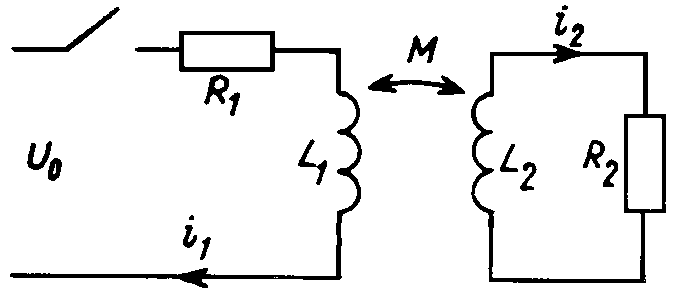
Рис. 17.3
Рассмотрим переходный процесс при подключении к источнику напряжения u0 трансформатора с индуктивностями обмоток L1, L2 и взаимной индуктивностью М, вторичная обмотка которого замкнута на сопротивление R2 (рис. 17.3).
17.4. ОСОБЕННОСТИ РАСЧЕТА ПЕРЕХОДНЫХ ПРОЦЕССОВ В ЦЕПЯХ С ИНДУКТИВНО СВЯЗАННЫМИ ЭЛЕМЕНТАМИ
|
|
Рассмотрим переходный процесс при подключении к источнику напряжения u0 трансформатора с индуктивностями обмоток L1, L2 и взаимной индуктивностью М, вторичная обмотка которого замкнута на сопротивление R2 (рис. 17.3). |
Процесс описывается уравнениями, составленными для обоих контуров относительно первичного и вторичного токов i1 и i2:

или
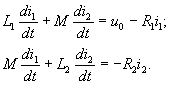
Для приведения системы к нормальной форме разрешим ее относительно производных обоих токов:

| (17.2) |
Для неидеального трансформатора — при L1L2 > М2 (коэффициент связи
![]() ) — из полученных уравнений состояния определим далее параметры общих решений обоих уравнений:
) — из полученных уравнений состояния определим далее параметры общих решений обоих уравнений:
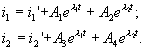
При действии на входе цепи постоянного источника u0 = U0 = соnst имеем в установившемся режиме: i1’= U0 /R1; i2’ = 0.
Корни l1,2 определим из характеристического уравнения, которое после раскрытия характеристического определителя приводится к виду
![]()
или
![]()
где a1 = R1/L1, a2 = R2/L2.
Имеем

откуда следует, что оба корня вещественны, и при любых соотношениях параметров один из корней меньше
![]()
Используя начальные условия для тока i1, получаем систему:
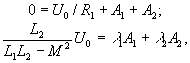
откуда находим постоянные интегрирования, которые с использованием связей между корнями характеристического уравнения приведем к виду:
![]()
Аналогично определяем и константы A3 и A4, входящие в решение для вторичного тока:

Здесь из первого уравнения следует, что A4 = – A3, из второго уравнения найдем A3 = – A4 = U0M/((l2 – l1)(L1L2 – M2)).
Таким образом, окончательное решение для токов в контурах имеет вид:
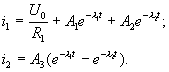
Характер изменения обоих токов при включении трансформатора изображен на рис. 17.4.

Рис. 17.4
Зависимость первичного тока i1(t) монотонная. При сильной связи контуров (k »
1) начальная часть переходного процесса характеризуется быстрым увеличением тока i1, а затем скорость его нарастания замедляется. Вторичный ток имеет форму апериодического импульса. Представляет интерес оценка влияния вторичного тока на процесс в первичном контуре. Для сравнения на рис. 17.4 изображена также кривая i1(t) при разомкнутой вторичной обмотке (при R2 = ∞), когда для тока имеем выражение ![]() ,
определяющее переходный процесс в последовательной RL-цепи (см.
п. 15.3). Из рисунка видно, что при нагрузке на R2 начальная часть кривой i1(t) характеризуется более быстрым ростом, чем при R2 = ∞, а в последующем рост первичного тока замедляется по сравнению с током i1 при разомкнутой вторичной обмотке. Нетрудно заметить, что интеграл от свободного тока
,
определяющее переходный процесс в последовательной RL-цепи (см.
п. 15.3). Из рисунка видно, что при нагрузке на R2 начальная часть кривой i1(t) характеризуется более быстрым ростом, чем при R2 = ∞, а в последующем рост первичного тока замедляется по сравнению с током i1 при разомкнутой вторичной обмотке. Нетрудно заметить, что интеграл от свободного тока ![]() , взятый за все время переходного процесса при конечном значении R2 и R2 = ∞ одинаков и вообще не зависит от характера нагрузки трансформатора. Действительно, из первого уравнения исходной системы имеем для свободного тока i1” = – [L1(di1”/dt) + M(di2”/dt)]/R1. Поэтому рассматриваемый интеграл равен
, взятый за все время переходного процесса при конечном значении R2 и R2 = ∞ одинаков и вообще не зависит от характера нагрузки трансформатора. Действительно, из первого уравнения исходной системы имеем для свободного тока i1” = – [L1(di1”/dt) + M(di2”/dt)]/R1. Поэтому рассматриваемый интеграл равен
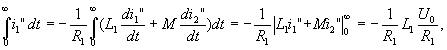
поскольку начальные значения свободных токов i1”(0) = U0/R1, i2”(0) = 0, а в установившемся режиме при t = ∞ оба свободных тока равны нулю. В связи с этим изображенные на рис. 17.4 кривые первичного тока пересекаются — вначале размагничивающее действие вторичного тока способствует ускоренному нарастанию первичного тока, а в последующем его влияние имеет противоположный характер.
Проанализируем также частный случай рассматриваемой задачи при идеальной связи контуров
— при k = 1 или ![]() . В этом случае в полученных выше уравнениях состояния в нормальной форме (17.2) члены с производными имеют теперь нулевые сомножители: L1L2 – М2 = 0, и эти уравнения приводят к алгебраической связи между обоими токами. С учетом соотношения между индуктивностями любое из рассматриваемых уравнений позволяет получить
. В этом случае в полученных выше уравнениях состояния в нормальной форме (17.2) члены с производными имеют теперь нулевые сомножители: L1L2 – М2 = 0, и эти уравнения приводят к алгебраической связи между обоими токами. С учетом соотношения между индуктивностями любое из рассматриваемых уравнений позволяет получить
![]()
Это означает, что в данном случае оба тока не играют роль переменных состояния, так как переменные состояния должны быть линейно независимыми. Полученная алгебраическая связь позволяет исключить ток ![]() из исходной системы, в результате чего
ее первое уравнение приводится к виду
из исходной системы, в результате чего
ее первое уравнение приводится к виду
![]()
Таким образом, для тока i1 имеем уравнение первого порядка. Поскольку единственный корень характеристического уравнения теперь равен ![]() то общее решение полученного дифференциального уравнения имеет вид
то общее решение полученного дифференциального уравнения имеет вид
![]()
Очевидно, что начальные условия для определения постоянной А не сохраняются равными i1(0) = 0; i2(0) = 0, так как это противоречит полученной связи между обоими токами. Понятно, что к обоим токам обмоток трансформатора с идеальной связью закон коммутации неприменим, так как он получен из условия непрерывности энергии магнитного поля катушки, а в трансформаторе обе обмотки имеют общее магнитное поле, и условие непрерывности должно относиться к суммарной энергии, которая определяется выражением ![]() Для трансформатора с идеальной связью это выражение можно привести к виду
Для трансформатора с идеальной связью это выражение можно привести к виду ![]() , откуда вытекает, что из условия непрерывности энергии магнитного поля в момент коммутации Wм(–0) = Wм (+0) теперь вовсе не следует условие непрерывности токов, а лишь связь между токами
, откуда вытекает, что из условия непрерывности энергии магнитного поля в момент коммутации Wм(–0) = Wм (+0) теперь вовсе не следует условие непрерывности токов, а лишь связь между токами
![]() или
или ![]()
Использование этого условия, заменяющего закон коммутации, вместе с алгебраическим соотношением, связывающим токи обмоток, полученным ранее, позволяет найти начальные значения обоих токов:

Теперь нетрудно определить выражения для токов переходного процесса, используя начальное условие и общее решение при t = 0:
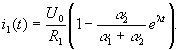
Из условия, связывающего токи, получим
![]()
Таким образом, при идеальной связи контуров (k = 1) быстрая начальная часть переходного процесса сокращается до нуля — при t = 0 токи скачком принимают указанные начальные значения, а затем изменяются по экспоненциальному закону, приближаясь к установившимся значениям.
Отметим еще раз, что токи идеализированных контуров не могут выступать в качестве переменных состояния: они не являются независимыми и в момент коммутации могут изменяться скачком. Условие непрерывности при t = 0 сохраняется для потокосцеплений обмоток. Действительно, поскольку ![]() а
а ![]()
то видно, что для этих величин непрерывность при t = 0 имеет место. Сами потокосцепления при идеальной связи пропорциональны друг другу: ![]() Поэтому в качестве переменных состояния при расчете переходных процессов контуров с k = 1 удобнее использовать потокосцепление одной из обмоток, а не их токи.
Поэтому в качестве переменных состояния при расчете переходных процессов контуров с k = 1 удобнее использовать потокосцепление одной из обмоток, а не их токи.
Исходную систему уравнений можно при этом переписать. в виде:

Вместе с уравнением ![]() они образуют систему уравнений относительно
Ψ1, i1 и i2, при интегрировании которой не возникает затруднений.
они образуют систему уравнений относительно
Ψ1, i1 и i2, при интегрировании которой не возникает затруднений.
Потокосцепления обоих контуров Ψ1 и Ψ2 можно использовать в качестве переменных состояния для расчета переходных процессов и в общем случае — для контуров с k < 1, когда оба потокосцепления не зависят друг от друга.