17.3. О ХАРАКТЕРЕ ПЕРЕХОДНЫХ ПРОЦЕССОВ В ЛИНЕЙНЫХ ЦЕПЯХ
Из приведенных выше примеров
следует, что токи и напряжения при переходном процессе в цепи n-го порядка, описываемой n уравнениями состояния, x(t) выражаются суммой вынужденной составляющей x'(t), обусловленной источниками, и свободной составляющей x"(t), представляющей при отсутствии кратных корней сумму экспонент ![]() , в показатели которых входят корни характеристического уравнения
lk
, в показатели которых входят корни характеристического уравнения
lk
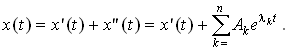
Расположение корней lk на комплексной плоскости, обозначенных крестиками на рис. 17.1, а, определяет характер слагаемых свободной составляющей.
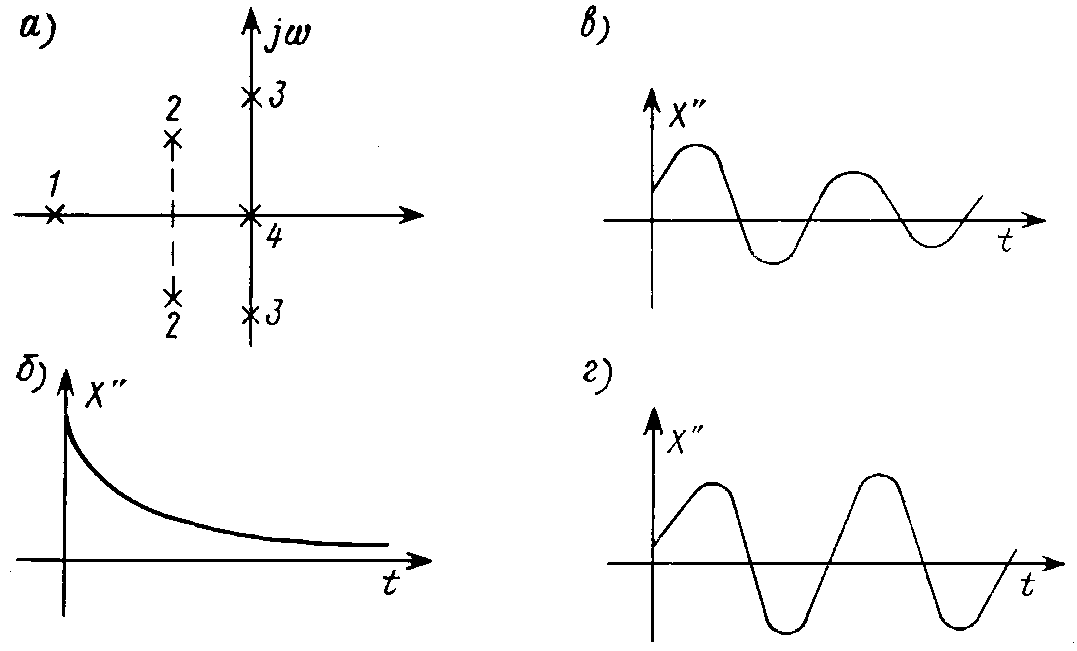
Рис. 17.1
Простые вещественные корни lk = – a (точка 1 на рис. 17.1, а) определяют экспоненциально затухающие апериодические слагаемые свободной составляющей A e–at (рис. 17.1, б). Комплексные сопряженные пары корней lk = – d ± jw' (точки 2 на рис. 17.1, а) дают экспоненциально затухающие колебательные составляющие (рис. 17.1, в)
![]()
Чисто мнимые пары корней (точки 3 на рис. 17.1, а) обусловливают незатухающие синусоидальные колебания A sin (wt + q) (рис. 17.1, г).
Свободный процесс в пассивной цепи с потерями носит затухающий характер, что связано с рассеянием энергии в резистивных элементах цепи. Поэтому для таких цепей имеем лишь вещественные отрицательные и комплексно сопряженные корни с отрицательной вещественной частью (точки 1 и 2 на рис. 17.1, а). Сопряженный характер корней определяется тем, что характеристическое уравнение имеет вещественные коэффициенты. Так как колебательный характер свободных составляющих x"(t) связан с периодическим обменом энергией между катушками и конденсаторами цепи, то комплексно сопряженные корни описывают процессы в пассивных цепях с RLC-элементами. При приближении пары комплексно сопряженных корней к мнимой оси интенсивность затухания колебательного процесса, выражаемая декрементом D, уменьшается. Как будет показано в Лекции 22, пассивные цепи с элементами RC и RL описываются лишь простыми вещественными корнями. LC-цепи также характеризуются простыми чисто мнимыми корнями. Кратные корни могут встретиться при описании процессов в пассивных RLC-цепях.
Если пассивная цепь с исключенными источниками, отвечающая свободным составляющим переходного процесса, имеет емкостные сечения (простейший случай — последовательно включенные конденсаторы) или индуктивные контуры (например, при параллельно соединенных катушках), то свободная составляющая в таких цепях содержит постоянное слагаемое, которому отвечает нулевой корень lk = 0 (точка 4 на рис. 17.1, а). Физический смысл таких составляющих определяется тем, что при наличии емкостного сечения в цепи возможно сколь угодно длительное существование постоянного заряда на конденсаторах сечения, а в индуктивном контуре возможно сколь угодно длительное протекание постоянного тока. Постоянные слагаемые в таких цепях появляются лишь в выражениях для напряжений конденсаторов емкостного сечения или токов индуктивного контура. В выражения других токов и напряжений той же цепи эти слагаемые не входят. Существование таких решений связано с идеализацией свойств элементов цепи — пренебрежением потерями в реальных катушках и проводимостью утечки реальных конденсаторов. В активных цепях, включающих управляемые источники, возможно появление неустойчивых, нарастающих во времени составляющих переходного процесса. Этот вопрос будет рассмотрен в Лекции 23.
В простейших цепях ограниченное число корней полностью определяет характер переходного процесса. Так, процесс в цепи первого порядка не может быть колебательным, так как такому процессу соответствует комплексно-сопряженная пара. Процессы в цепи второго порядка носят либо апериодический (при вещественных различных или кратном корнях), либо колебательный характер (при комплексно сопряженных корнях).
В пассивной цепи третьего порядка один корень характеристического уравнения всегда отрицательный вещественный, а два других либо образуют комплексно сопряженную пару, либо также являются отрицательными вещественными. Соответственно и свободные составляющие переходного процесса содержат апериодические слагаемые и не более одного колебательного слагаемого. В цепях более высокого порядка возможны несколько видов собственных колебаний, которым отвечают различные пары комплексно сопряженных корней, а также несколько апериодических составляющих, соответствующих различным вещественным корням.
В пассивных цепях, все корни которых имеют отрицательные вещественные части (точки 1 и 2 на рис. 17.1, а), переходный процесс имеет затухающий характер, и установившийся режим x'(t) при t ® ¥ не зависит от начальных условий, а определяется лишь структурой и элементами цепи и действующими в ней источниками. С другой стороны, свободные составляющие переходного процесса x"(t) существенно зависят от условий, имеющих место в цепи в момент коммутации — при t = 0. При определенных начальных условиях отдельные свободные слагаемые могут отсутствовать — соответствующие им постоянные Ak равны нулю. Возможно, в частности, такое сочетание начальных условий и параметров внешних источников, при котором начальные значения всех переменных состояния x(0) равны значениям установившихся решений в этот момент времени х'(0). В таких случаях переходная составляющая x"(t) равна нулю, и в цепи сразу с момента коммутации t = 0 наступает установившийся режим. Возможность подобных ситуаций в простейших RC- и RL-цепях была установлена ранее в п. 15.2 и 15.3.