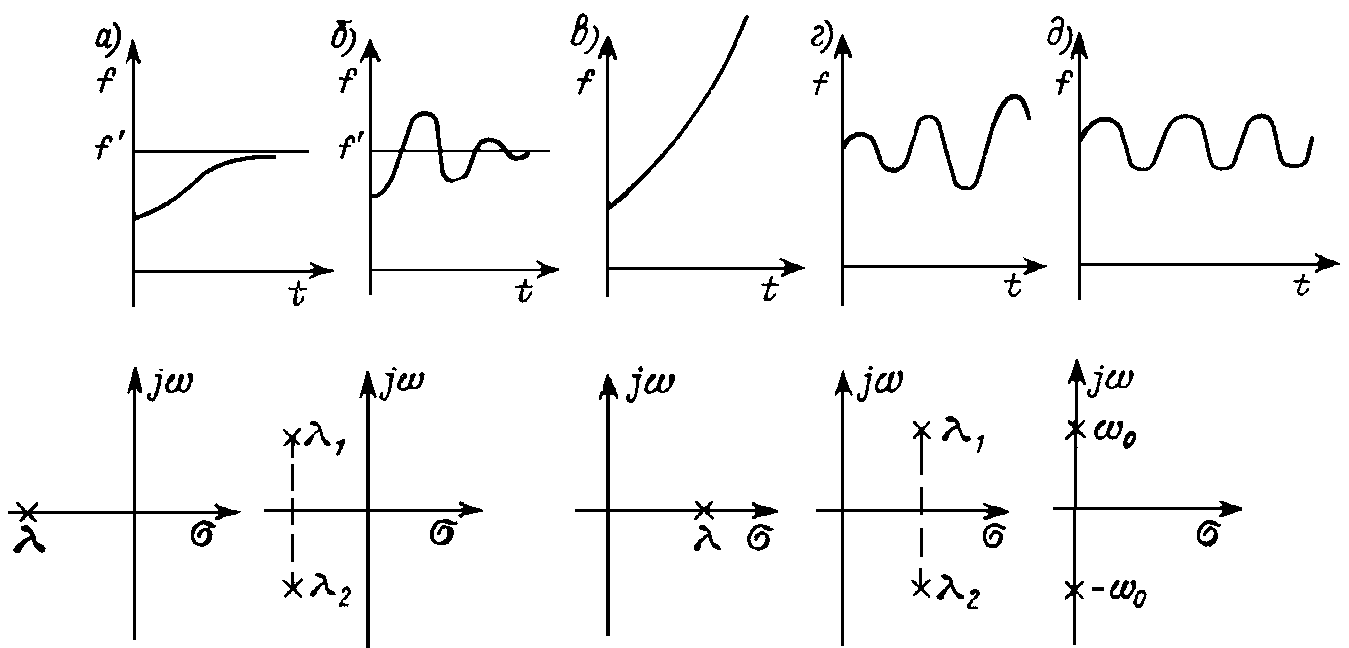
23.1. УСТОЙЧИВОСТЬ ЭЛЕКТРИЧЕСКИХ ЦЕПЕЙ
В устойчивой электрической цепи при ограниченном возмущении переходный процесс, возникающий в цепи, с течением времени затухает, и токи и напряжения в цепи f(t) переходят к новому установившемуся режиму — положению равновесия f ' (рис. 23.1, а,б). В неустойчивой цепи процесс отклонения от равновесия с течением времени нарастает (рис. 23.1, в, г).
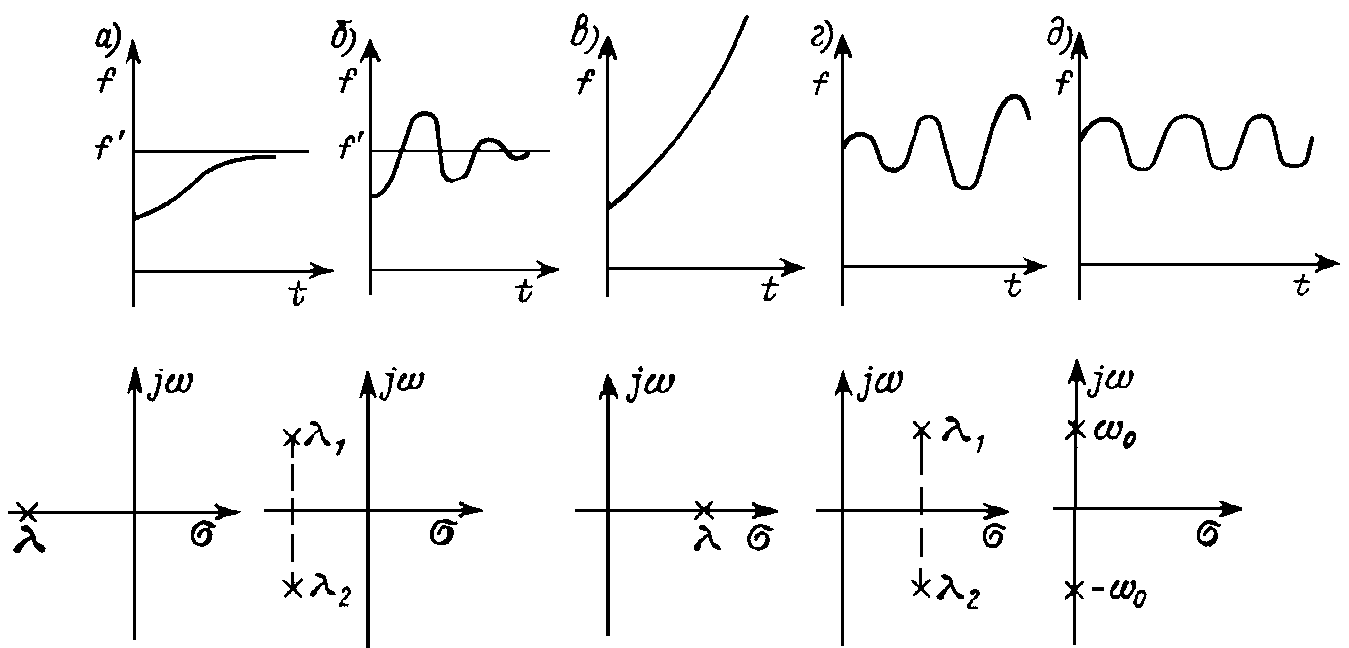
Рис. 23.1
Напомним, что аналитические решения для токов и напряжений переходного процесса в линейной цепи при простых корнях характеристического уравнения
lk имеют вид 
(f
' — установившееся значение). Поэтому в устойчивой цепи, в которой свободная составляющая
f" стремится с течением времени к нулю, все вещественные корни характеристического уравнения должны быть отрицательными (рис. 23.1, а), а комплексные — иметь отрицательную вещественную часть (рис. 23.1, б). Это же относится к кратным корням, и в устойчивой цепи все корни характеристического уравнения (полюсы передаточной функции) удовлетворяют общему условию
,
т. е. на комплексной плоскости s + jw они лежат в левой полуплоскости. Если хотя бы один из корней располагается в правой полуплоскости (рис. 23.1, в, г), цепь является неустойчивой.
Устойчивыми являются пассивные цепи, составленные из R-, L-, С-элементов. Цепи без потерь (включающие только L и С) находятся на границе устойчивости, поскольку их характеристические уравнения имеют чисто мнимые корни, отвечающие собственным частотам цепи w0. Такое положение корней обусловливает незатухающий переходный процесс при произвольном возбуждении (рис. 23.1, д). Однако в случае синусоидального возбуждения цепи без потерь на собственной частоте w = w0 ограниченное по амплитуде входное воздействие приводит к неограниченной реакции — в общем решении для f(t) в этом случае появляются слагаемые вида telkt, неограниченно нарастающие во времени при lk = ± jw0. Поэтому цепи, имеющие полюсы на мнимой оси, являются неустойчивыми в том смысле, что их выходная величина может быть неограниченной при подаче на вход вполне определенного сигнала с ограниченной амплитудой.
Неустойчивость может наблюдаться в активных цепях с обратными связями, в которых энергия, накапливаемая пассивными элементами при переходном процессе, восполняется управляемыми источниками, что может привести к неограниченному росту токов и напряжений при ограниченном входном воздействии.
Потеря устойчивости ведет к нарушению заданного режима работы цепи, и поэтому для обеспечения устойчивого режима работы цепи необходимо провести исследование ее устойчивости. Однако работа на границе устойчивости при чисто мнимой паре корней — автоколебательный режим — на практике используется для построения генераторов. Как следует из названия, автоколебания — это незатухающие колебания в цепи с потерями при отсутствии внешних периодических воздействий, обусловленные внутренними свойствами цепи.
При анализе устойчивости определяют расположение корней характеристического уравнения на комплексной плоскости. При этом нет необходимости непосредственно находить значения корней, а достаточно убедиться в их отсутствии в правой полуплоскости.
Для характеристического уравнения второго порядка a0l2 + a1l + a2 = 0 условия устойчивости формулируются наиболее просто. Так как, согласно теореме Виета, l1 + l2 = – a1/a0, а l1l2 = a2/a0, то при a0 > 0 l1 и l2 располагаются в левой полуплоскости при выполнении условий a1 > 0, a2 > 0. Таким образом, необходимым и достаточным условием устойчивости цепи 2-го (а также и 1-го) порядка является положительность значений всех коэффициентов характеристического уравнения.
Обратим внимание, что при a1 = 0
цепь находится на границе устойчивости, Так
как в этом случае корни характеристического уравнения чисто мнимые
, где 
,
при a1 = 0 в цепи наблюдается синусоидальный колебательный режим с круговой частотой
w0.
Для характеристического уравнения более высокого порядка положительность коэффициентов ak > 0 является необходимым, но не достаточным условием устойчивости. Поэтому для проверки условия Re lk ³ 0 применяют способы, использующие так называемые критерии устойчивости, не требующие непосредственного определения корней.
Одним из таких критериев, позволяющих оценивать устойчивость по алгебраическим признакам (по коэффициентам характеристического уравнения), является критерий Гурвица. При его использовании для исследования расположения корней характеристического уравнения n-го порядка
составляют так называемый определитель Гурвица
На главной диагонали определителя п-го порядка в возрастающем порядке стоят коэффициенты характеристического уравнения от a0 до an. Далее в строках располагают подряд в порядке убывания индексов остальные коэффициенты; позиции в строке справа от a0 и слева от an дополняются нулями. Так, в нулевой строке стоит только элемент a0, в первой строке — лишь три ненулевых элемента a2, a1, a0, а в последней — только один элемент an.
Гурвиц доказал, что положительность определителя Dn и всех его диагональных миноров Dk, отчеркнутых в приведенном выражении Dn, является необходимой и достаточной для того, чтобы все корни характеристического уравнения lk лежали в левой полуплоскости. Таким образом, для исследования устойчивости системы, описываемой характеристическим уравнением п-го порядка, необходимо проверить выполнение условий:
, 
, …, 
, 
.
Применение критерия Гурвица к уравнению 2-го порядка требует анализа положительности определителя
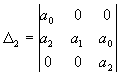= a0a1a2 и его миноров
D0 = a0, D1 = a0a1, что приводит к уже ранее установленным условиям
a0 > 0; a1 > 0; a2 > 0.
Определитель Гурвица 3-го порядка имеет вид
.
Его миноры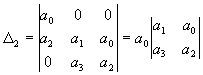 
; D1 = a1a0; D0 = a0. Поэтому расположение корней в левой полуплоскости обеспечивается при
a0 > 0, a1 > 0, a1a2 – a0a3 > 0, D3 = a3D2. Таким образом, кроме необходимой положительности коэффициентов а2 > 0, а3 > 0 имеем дополнительное условие
a1a2 – a0a3 > 0. Отсюда следует, что для уравнений 3-го
положительность коэффициентов не гарантирует расположения корней в левой полуплоскости.
То же справедливо и в отношении уравнений более высоких порядков.
Другие критерии основаны на анализе частотных свойств цепей и описывающих их функций. Для выяснения устойчивости согласно критерию Михайлова, на комплексной плоскости изображают годограф характеристического полинома
H(s) при s = jw
— его амплитудно-фазовую частотную характеристику
H(jw) = a0(jw)n + a1(jw)n–1 + ... + an, соответствующую изменению частоты от нуля до бесконечности. Если эта характеристика последовательно проходит в направлении против часовой стрелки п квадрантов плоскости комплексного переменного Н, полином соответствует устойчивой цепи. В этом случае при движении по характеристике от
w = 0 к
Рис. 23.2
Так как АФЧХ H(jw) является конформным отображением мнимой оси плоскости s = s + jw, осуществляемым функцией Н(s), то эта функция отображает в начало координат лишь точки плоскости s, находящиеся слева от мнимой оси, т. е. имеющие отрицательные вещественные части Re s < 0. Прохождение амплитудно-фазовой характеристики H(jw) через начало координат (кривая 2) отвечает наличию пары чисто мнимых корней. Нарушение последовательности обхода квадрантов, при котором начало координат обходится справа (кривые 3, 4, 5), отвечает неустойчивости цепи — наличию корней в правой полуплоскости. Из рассмотренного критерия следует также, что у характеристического полинома H(jw) = H1(w) + jH2(w) устойчивой цепи нули вещественной и мнимой частей H1(w) и H2(w) чередуются между собой подобно нулям и полюсам (нулям знаменателя) входной функции цепи без потерь. Именно это свойство характеристического полинома положено в основу вывода критерия Гурвица.
Примеры анализа устойчивости по характеристическим уравнениям рассмотрены в задаче 21.1.
