Проанализируем устойчивость активной интегрирующей цепи с идеальным усилителем с конечным коэффициентом усиления (рис. 23.3, a).

Рис. 23.3

Узловое уравнение для операторных изображений напряжений имеет вид

.

Так как входное и выходное напряжения усилителя связаны условием U₃(s) = kU₂(s), то для выходного напряжения U₃(s) получим

.

Отсюда следует, что единственный корень характеристического уравнения находится в левой полуплоскости при k < 1. Это и есть условие устойчивости данной цепи. Поэтому при ее использовании в качестве интегрирующей ветвь обратной связи необходимо подключить к инвертирующему входу усилителя (рис. 23.3, б): устойчивость цепи достигается при любом отрицательном значении коэффициента усиления усилителя. Подключение цепи обратной связи к неинвертирующему входу не позволит обеспечить нормальную устойчивую работу интегрирующей цепи.

Выясним условия устойчивой работы активного звена фильтра нижних частот (рис. 23.4, а). Запишем уравнения для узлов 2 и 3:

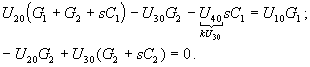
Характеристическое уравнение получим, приравняв к нулю главный определитель системы

.

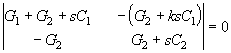Окончательно можно записать .

Необходимое и достаточное условие устойчивости для цепи 2-го порядка сводится к положительности значений коэффициентов, что обеспечивается при выполнении неравенства

.

Следовательно, для устойчивой работы цепи необходимо, чтобы коэффициент усиления k не превышал значения C₂(G₁ + G₂)/(C₁G₂) + 1 или для равных значений C₁ = C₂ = C, G₁ = G₂ = G = 1/R, схема фильтра устойчива при k < 3. Если k = 3, то характеристическое уравнение имеет чисто мнимые корни l_1,2 = ± j 1/RC. В этом случае звено можно использовать в качестве генератора: при закороченном входе (рис. 23.4, б) на выходе цепи будем иметь синусоидальные автоколебания с круговой частотой w₀ = 1/RC.

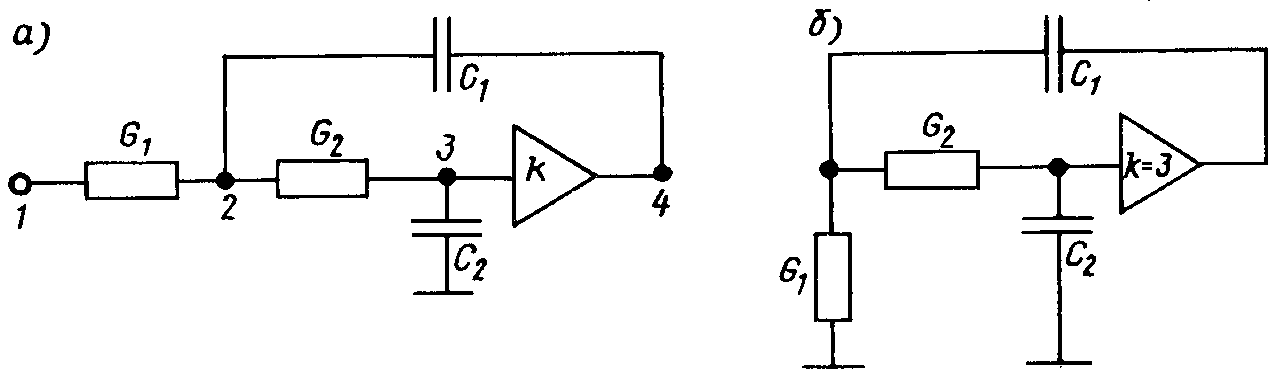
Рис. 23.4

Пример анализа устойчивости активной цепи рассмотрен в задаче 21.2.