


23.3. УСЛОВИЯ ГЕНЕРАЦИИ СИНУСОИДАЛЬНЫХ АВТОКОЛЕБАНИЙ В АКТИВНЫХ ЦЕПЯХ
Рассмотрим требования к элементам цепи, генерирующей синусоидальные автоколебания на частоте
w0. Такая цепь включает в себя усилитель напряжения
k (рис. 23.5) и пассивную цепь обратной связи с передаточной функцией
b(s) = U1(s)/U2(s).
|
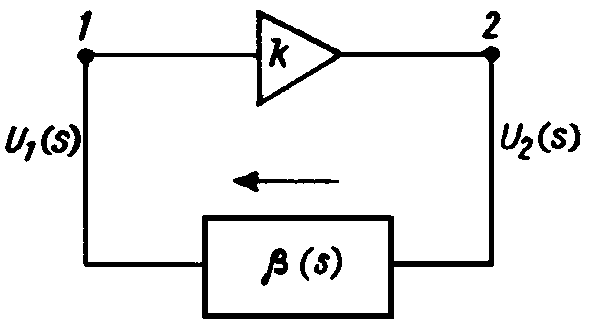
Рис. 23.5
|
Следует обратить внимание, что эта цепь передает сигнал в направлении изображенной на рисунке стрелки, и поэтому ее входное напряжение есть
U2(s), а выходное
— U1(s). Поскольку оба эти напряжения связаны также условием
U2(s) = kU1(s), то режим генерации синусоидальных колебаний (s = jw0) обеспечивается при выполнении соотношения
 или или
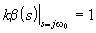 . .
|
Разделяя в последнем равенстве вещественную и мнимую части, получим условия баланса фазы и амплитуды:
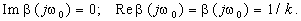
Таким образом, цепь обратной связи на частоте генерации должна обеспечивать фазовый сдвиг между входным и выходным сигналами
q = 0 или 180°, а ослабление амплитуды сигнала на этой частоте цепью обратной связи
b(jw0) должно компенсироваться соответствующим подбором значения коэффициента усиления
k. При q = 0 коэффициент усиления
k > 0, а при q = 180°
k < 0, т. е. в этом случае усилитель должен обладать инвертирующим свойством.
Рассмотрим RС- и LC-генераторы. Из условий баланса следует, что цепи первого порядка нельзя использовать в качестве цепей обратной связи в генераторах, так как они не обеспечивают требуемый сдвиг фаз q на конечных частотах. Не подходят по тем же причинам и RС-цепи 2-го порядка с характеристиками фильтра верхних или нижних частот (рис. 23.6, а,б).
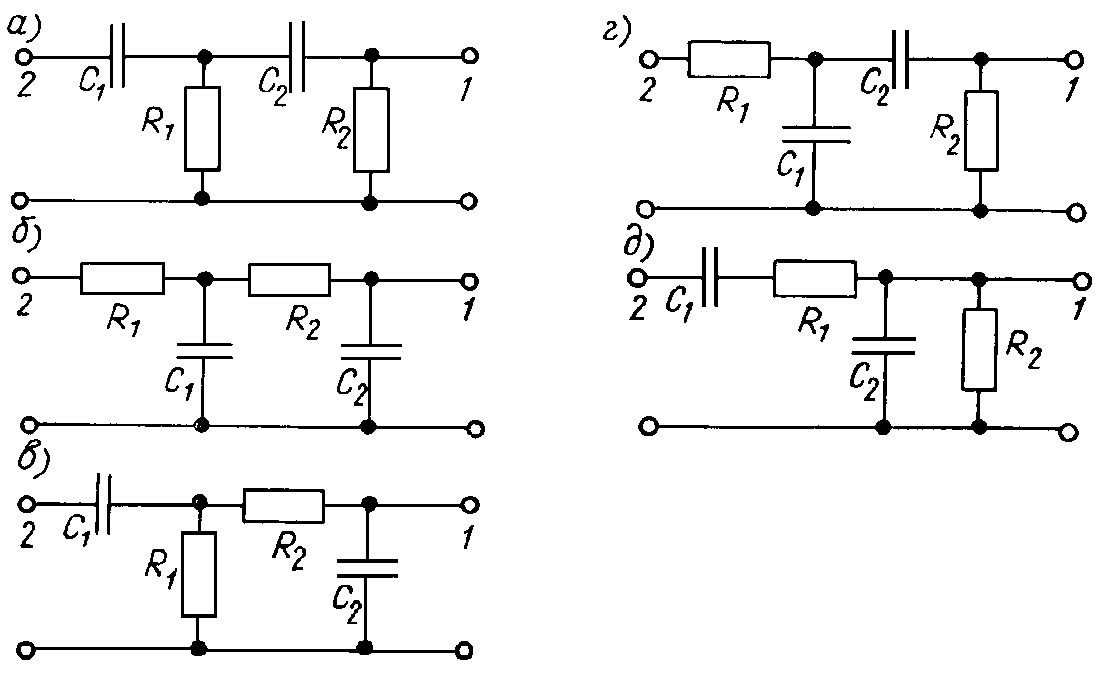
Рис. 23.6
Однако цепи, обладающие частотными характеристиками полосового фильтра (рис. 23.6, в – д), могут обеспечить необходимые требования. Это следует, в частности, из того, что поскольку такие цепи 2-го порядка не пропускают сигналы ни при
w = 0, ни при w = ¥, то общее выражение их передаточной функции имеет вид
 .
.
На частоте s = jw, при которой достигается компенсация членов
a0s2 + a2 = 0 т. е. 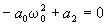 или
или  , передаточная функция цепи обратной связи становится вещественной
, передаточная функция цепи обратной связи становится вещественной
 , и поэтому нахождение коэффициентов передаточной функции
a0, a1 и a2 цепи обратной связи, по существу, и решает задачу определения параметров генератора. При этом коэффициент усиления усилителя равен
k = a1.
, и поэтому нахождение коэффициентов передаточной функции
a0, a1 и a2 цепи обратной связи, по существу, и решает задачу определения параметров генератора. При этом коэффициент усиления усилителя равен
k = a1.
Иной распространенной схемой RС-генератора является схема с цепью обратной связи 3-го порядка (рис. 23.7).
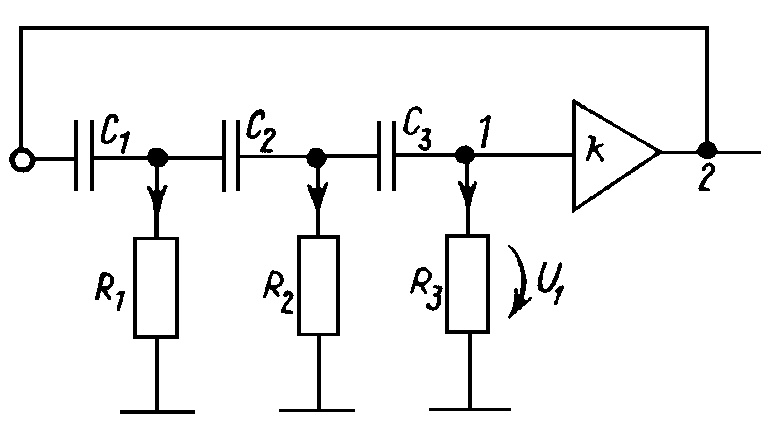
Рис. 23.7
Ее передаточная функция имеет общее выражение
 ,
,
или при s = jw
 .
.
В этом случае частоту генерации определяют из условия вещественности передаточной функции
– a1w2 + a3 = 0, или
 , а коэффициент усиления — из условия баланса амплитуд k = 1/b(jw0) = (a0a3 – a1a2)/a0a3.
, а коэффициент усиления — из условия баланса амплитуд k = 1/b(jw0) = (a0a3 – a1a2)/a0a3.
При равенстве параметров элементов цепи обратной связи
C1 = C2 = C3 = C и
R1 = R2 = R3 = R, что обычно и используется на практике, передаточную функцию цепи обратной связи определим следующим образом. Так как IR33 = IC33 = U1/R, то
 . Выразим через введенные величины напряжение
. Выразим через введенные величины напряжение
 . Ток
. Ток 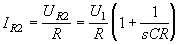 , а ток
, а ток
 . Поэтому напряжение
. Поэтому напряжение
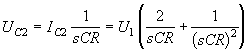 . Подобным образом находим далее
. Подобным образом находим далее
 и
и 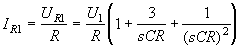 . Это позволяет получить ток
. Это позволяет получить ток
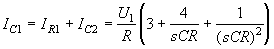 . Окончательно рассчитаем напряжение на входе цепи обратной связи:
. Окончательно рассчитаем напряжение на входе цепи обратной связи:
 , что приводит к следующему выражению для передаточной функция цепи обратной связи
, что приводит к следующему выражению для передаточной функция цепи обратной связи
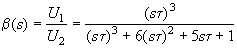 ,
,
где t = RC.
Таким образом, коэффициенты передаточной функции в рассматриваемом случае равны
a0 = t3; a1 = 6t2; a2 = 5t; a3 =
1; для частоты автоколебаний генератора имеем
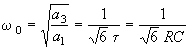 , а коэффициент усиления
k равен
, а коэффициент усиления
k равен  .
.
В схемах обратных связей генераторов используются также резонансные контуры с индуктивными катушками. В одной из простейших схем LС-генератора (рис. 23.8, а) вещественность передаточной функции цепи обратной связи обеспечивается на частоте резонанса LС-контура
ω0 = 1/ЦLC, когда токи в ветвях этого контура взаимно компенсируются, и передаточная функция b(jw0) равна R2/(R1 + R2). Отсюда следует, что коэффициент усиления усилителя
k = 1/b(jw0)
= 1 + R1/R2. Расчет характеристик
w0 и k других схем LC-генераторов с неполным включением катушки (рис. 23.8, б), конденсатора (рис. 23.8, в) и взаимной индуктивностью (рис. 23.8, г). изображенных на рис. 23.8 генераторов проводят аналогично.
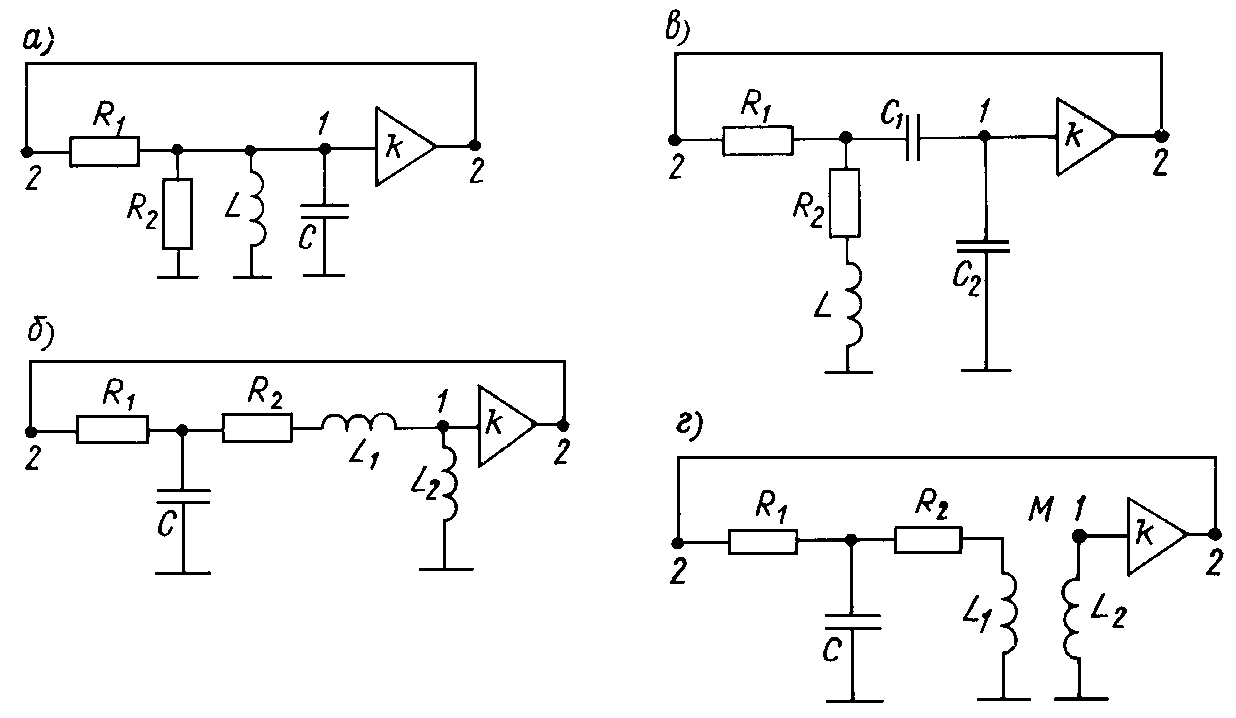
Рис. 23.8
Конец 23-й лекции
Обратно к плану данной лекции
Перейти к задачам по теме данной лекции
Дальше к плану следующей лекции

![]() или
или
![]() .
.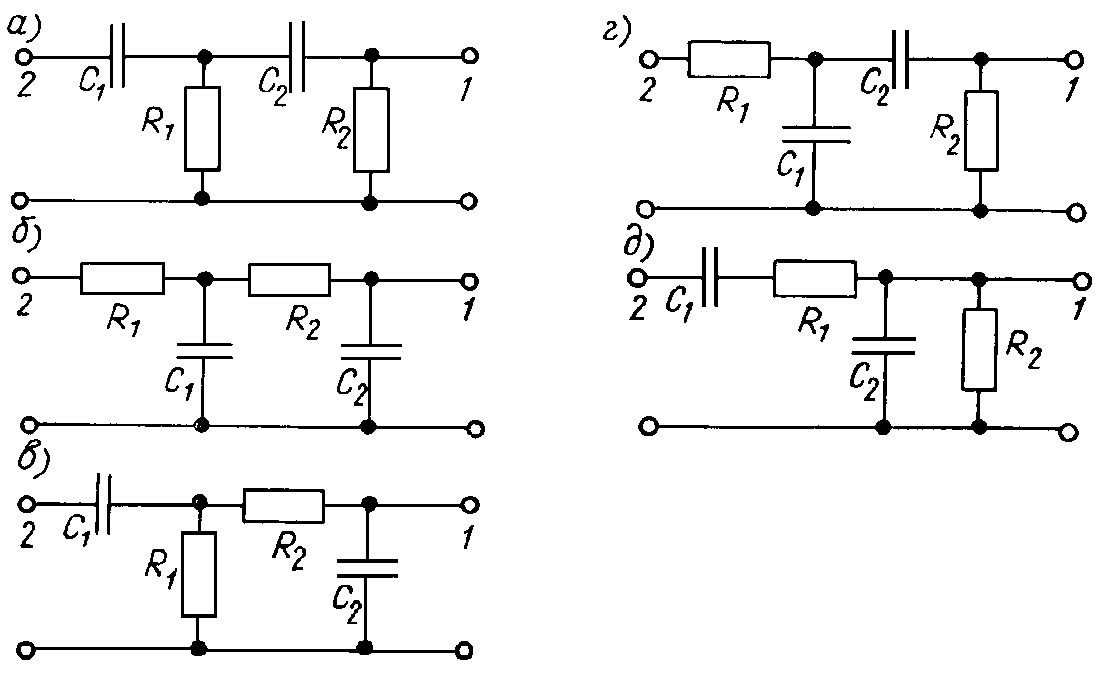

 .
.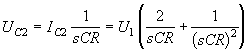 . Подобным образом находим далее
. Подобным образом находим далее
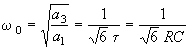 , а коэффициент усиления
k равен
, а коэффициент усиления
k равен 