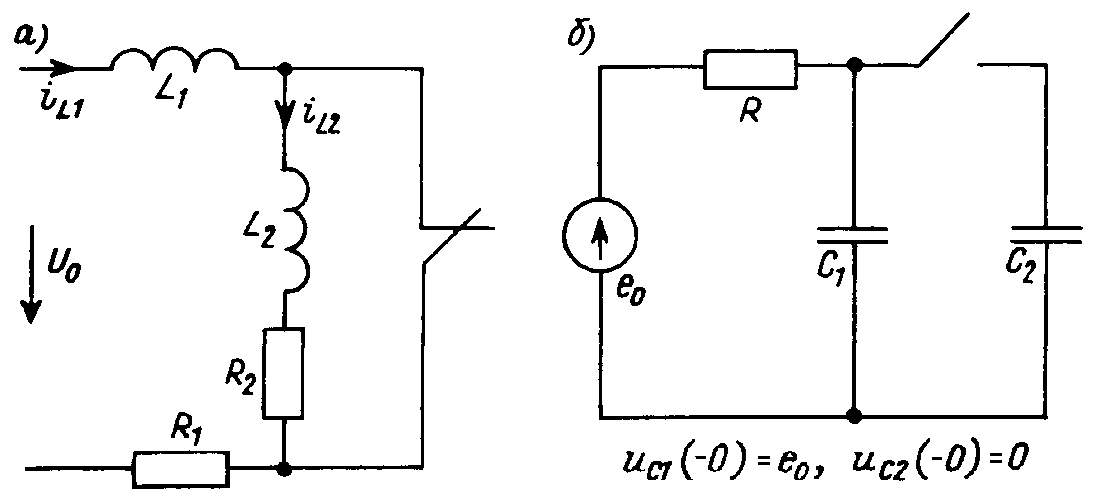
К достоинствам операторного метода относится также и то, что он позволяет по общей схеме рассчитывать переходные процессы в случаях, когда нарушаются законы коммутации — не соблюдается непрерывность токов в катушках и напряжений на конденсаторах. Нарушение непрерывности переменных состояния имеет место, если коммутация — замыкание или размыкание ключа — приводит к такому изменению структуры цепи, при котором образуются сечения из индуктивностей и источников тока, начальные значения токов которых не удовлетворяют первому закону Кирхгофа, или возникает контур из емкостей и источников ЭДС, напряжения в котором не удовлетворяют второму закону Кирхгофа. Простейшие схемы с примерами некорректных коммутаций изображены на рис. 19.9.

Рис. 19.9

В схеме, приведенной на рис. 19.9, а до размыкания ключа значения токов в обеих катушках L₁ и L₂ были неодинаковы: ; . После коммутации, в результате которой в цепь последовательно с индуктивностью L₁ вводилась индуктивность L₂, имеем . Следовательно, оба тока принципиально не могут сохраниться непрерывными в момент коммутации. Вследствие скачкообразного изменения токов напряжения на катушках в момент некорректной коммутации принимают бесконечно большие значения — они имеют характер импульсных функций.

Аналогично при подключении незаряженного конденсатора С₂ параллельно к заряженному С₁ (рис. 19.9,б) нарушается непрерывность напряжений на конденсаторах: , а . Этот процесс мгновенной перезарядки конденсаторов сопровождается протеканием бесконечно больших — импульсных — токов через конденсаторы.

Расчет таких переходных процессов на основе дифференциальных уравнений требует определения начальных значений токов i_L и напряжений u_C при . Для этого можно использовать условия непрерывности суммарного потокосцепления обеих катушек или условие непрерывности суммарного заряда конденсаторов . Однако применение операторного метода позволяет при использовании в расчете начальных условий переменных состояния до коммутации и не только получить импульсные составляющие напряжений и токов в цепи при , но определить их последующие изменения. При этом общая схема расчета цепи операторным методом при ненулевых начальных условиях полностью сохраняется.

Рассмотрим расчет переходного процесса в схеме, изображенной на рис. 19.9, б. С учетом указанных выше начальных условий эквивалентная операторная схема цепи имеет вид, показанный на рис. 19.10. Для напряжений , применяя метод узловых напряжений, получим

С помощью теоремы разложения найдем оригинал этого изображения

.

Отсюда видно, что , т.е. соблюдается отмеченная выше непрерывность суммарного заряда конденсаторов. До коммутации мы имели ; , а после коммутации: ; . Сумма зарядов и .

Для изображения тока в конденсаторе получим

.

Поскольку это выражение представляет неправильную дробь, ему соответствует оригинал, имеющий слагаемое в виде d-функции. Для его нахождения выделим целую часть изображения, которая определяет площадь d-импульса тока:

.

Оригинал второго слагаемого находим по теореме разложения

.

Это выражение показывает, что ток переходного процесса складывается из быстрой составляющей импульсного характера, обусловливающей мгновенную подзарядку конденсатора C₂ до напряжения , и последующей медленной — экспоненциальной — составляющей, определяющей дозарядку обоих параллельно включенных конденсаторов до напряжения источника e₀ (рис. 19.11).

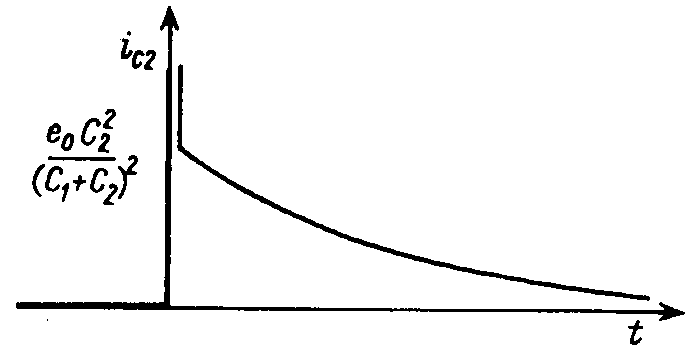
Рис. 19.11

Полученный результат связан с идеализацией свойств цепи — пренебрежением сопротивлением и индуктивностью контура, возникающего при замыкании ключа. При учете этих параметров, реально всегда отличных от нуля, токи в ветвях рассматриваемой цепи будут в течение всего переходного процесса иметь конечное значение. Однако расчетные соотношения для их определения будут более сложными — учет сопротивления контура приводит к описанию цепи уравнениями второго порядка, а учет индуктивности — уравнениями третьего порядка. Поэтому идеализация свойств цепи — пренебрежение параметрами и контура — упрощает расчет.

Необходимо обратить также внимание на то, что в момент некорректной коммутации нарушается непрерывность суммарной энергии, запасенной в электрическом поле обоих конденсаторов. Действительно, в рассмотренном случае (см. рис. 19.9, б) до коммутации энергия первого конденсатора , а . Непосредственно после коммутации и связанной с ней перезарядкой конденсаторов , а . Следовательно, суммарная энергия при коммутации уменьшается:

.

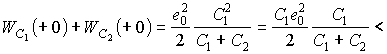
Последнее утверждение связано с тем, что часть энергии, тем не менее, тратится на необратимые процессы в контуре перезарядки. Несмотря на нулевое сопротивление цепи, выделение тепла в ее элементах при протекании бесконечно большого тока имеет место — мощность p = i²R, потребляемая при этом в контуре, бесконечна, и за бесконечно малый промежуток времени не изображенные на схеме элементы цепи успевают поглотить конечную часть энергии. В этом можно убедиться, рассматривая необратимое выделение энергии в контуре из конденсаторов с конечным сопротивлением R. При предельном переходе R ® 0 эта энергия сохраняет конечное значение.