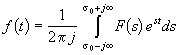19.6. ПЕРЕХОД ОТ ИЗОБРАЖЕНИЙ К ОРИГИНАЛАМ
Найти оригинал f(t) по его операторному изображению F(s) можно в общем случае по формуле обратного преобразования Лапласа
.
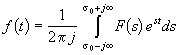Однако при расчете переходных процессов это выражение крайне редко используют непосредственно. Если изображение
F(s) представляет однозначную функцию переменной
s, и выполняется условие 
, то путь интегрирования в последнем интеграле можно считать замкнутым (штриховая линия на рис. 19.1) и воспользоваться для вычисления интеграла по замкнутому контуру теоремой о вычетах. Тогда
,
где sk — особые точки функции F(s), охваченные контуром интегрирования.
Обычно при расчете переходных процессов в цепях с сосредоточенными параметрами изображения
F(s) представляют собой дробно-рациональные функции с простыми полюсами и конечным пределом 
. Очевидно, это имеет место для правильной рациональной дроби 
. При выполнении указанного условия и отсутствии кратных полюсов
F(s) использование правила вычисления вычетов в простых полюсах приводит к выражению для оригинала
,
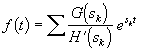где sk — корни знаменателя H(s) = 0; H '(s) = dH/ds; суммирование идет по всем полюсам.
Последняя формула называется также теоремой разложения. Примеры ее применения к нахождению оригиналов даны в Задачe 15.1 и Задачe 15.2
Если рациональная дробь F(s) имеет целую часть, что свидетельствует о том, что оригинал неограничен при
t ® 0, то необходимо выделить эту целую часть. Ей отвечает оригинал в виде
d-импульса 
. Остаток
F(s) представляет собой правильную дробь, к которой применяют теорему разложения. Соответствующий пример рассмотрен в
Задачe 15.2
Присутствие в операторном изображении сомножителей вида e-st свидетельствует о наличии в решении слагаемых, запаздывающих на время
t от начала исходного процесса
при t = 0. Алгебраические сомножители в таких слагаемых приводятся к оригиналу с помощью теоремы разложения, а при суммировании учитывается
их сдвиг на время
t. Например, при вычислении
оригинала функции F(s) = [s + a (1 – e-st)]/[s(s + a)]
рассмотрим сначала отдельно слагаемое F1(s) = (s + a )/[s(s + a)]
= 1/s.. Как известно из сводки основных формул (Приложениe 4), ему отвечает оригинал
в виде единичной функции. Второе слагаемое F2(s) = [–a(s + a )]e-st
имеет алгебраический сомножитель –a(s + a ), для которого с помощью теоремы разложения найдем 
. Так как
t' = t – t, то окончательно запишем 
. Соответствующая зависимость изображена на рис. 19.6.
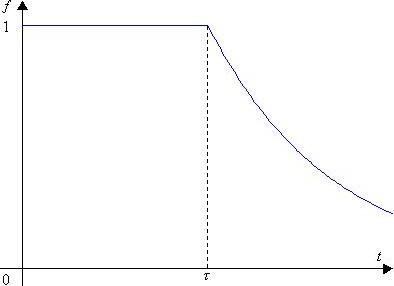
Рис. 19.6
Рассмотренные способы определения оригинала принципиально ограничены однозначными функциями F(s). Если изображение представляет собой многозначную функцию комплексной переменной s, имеющую точки разветвления, для нахождения оригинала следует использовать общую интегральную формулу обратного преобразования Лапласа. В теории цепей такие задачи возникают при рассмотрении цепей с распределенными параметрами или их моделей с бесконечным количеством сосредоточенных элементов, когда изображения содержат переменную s под знаком корня (например, при рассмотрении процессов в бесконечно длинных кабелях.
Перейти к задачам по теме данной лекции