Помимо свойства вещественности F(s) при вещественных s = s, функции входного сопротивления и проводимости пассивных цепей обладают дополнительным общим свойством. В правой полуплоскости входная функция F(s) аналитична — она не имеет там полюсов. На границе правой полуплоскости — на мнимой оси s = jw — вещественная часть F(s) неотрицательна: Re F(jw) ³ 0, поскольку Re Z(jw) = R(w) представляет собой эквивалентное активное сопротивление двухполюсника R(w), являющееся неотрицательной величиной, а Re Y(jw) = G(w) — эквивалентная активная проводимость, обладающая тем же свойством. Так как вещественная часть любой аналитической функции достигает минимальных значений на границе области, то во всей правой полуплоскости

при и .

(22.3)

Два общих условия — вещественности (22.2) и положительности (22.3) функции F(s) — определяют положительную вещественную функцию. Эти два условия являются необходимыми и достаточными для того, чтобы функцию F(s) можно было реализовать в виде двухполюсника, обладающего данным операторным входным сопротивлением Z(s) или проводимостью Y(s).

Проверка условия положительности в общем виде (22.3) достаточно трудоемка, поэтому ее часто заменяют анализом более простых частных условий: расположение полюсов и нулей — вещественных или комплексно сопряженных — в левой полуплоскости; нули на мнимой оси могут быть только простыми. Поскольку последнее относится к нулю и полюсу при s = ¥, то степени числителя и знаменателя входной функции не могут отличаться более, чем на единицу.

Если отмеченный характер расположения полюсов и нулей имеет место, то проверить условия положительности достаточно лишь для значений s = jw, так как при этом вследствие аналитичности условие положительности (22.3) в правой полуплоскости будет заведомо выполняться.

Пример проверки положительности функции рассмотрен в Задаче 20.2.

Дополнительными свойствами обладают цепи частного вида, составленные из двух типов пассивных элементов. Начнем их рассмотрение с входных функций цепей без потерь (LС-цепей). Эти функции имеют чисто мнимые корни числителя и знаменателя, так как переходный процесс в такой цепи из-за отсутствия потерь носит незатухающий характер. Группируя сомножители числителя и знаменателя, соответствующие сопряженным корням s_0k = ± jw_k, придем к выводу, что общий вид входной функции LС-цепи можно выразить формулой

(22.4)

Так как при s ® ¥ вся цепь без потерь приводится к одному конденсатору или катушке, то ее сопротивление в этом предельном режиме либо стремится к нулю, либо неограниченно возрастает. Поэтому степени числителя и знаменателя входной функции LС-цепи обязательно отличаются на единицу. Из приведенного выражения F_LC(s) следует также, что при нечетной степени полинома в числителе знаменатель представляет четный полином, и наоборот, при w₀ = 0 имеет четные степени в числителе F_LC(s) и нечетные — в знаменателе.

Следующее свойство цепей указанного класса состоит в чередовании полюсов и нулей F_LC(s) на мнимой оси. Рассматривая сопротивление при комплексных значениях s = s + jw, запишем его в виде F_LC(s + jw) = R(s, w) + jX(s, w). Вещественная и мнимая части аналитической функции Z_LC(s) связаны условием Коши - Римана: ¶R/¶s = ¶X/¶w. Так как на всей мнимой оси эквивалентное активное сопротивление цепи без потерь R(w) = 0, а в правой полуплоскости при всех s > 0 должно выполняться условие положительности (22.3) R(s, w) > 0, то на мнимой оси имеем ¶R/¶s > 0, а следовательно, ¶X/¶w > 0, и зависимость X(w) является монотонно возрастающей. Отсюда следует закон чередования полюсов и нулей функции Z(s) LС-цепи: при наличии двух нулей, не разделенных полюсом на мнимой оси, функция X(w) имела бы падающие участки с ¶X/¶ w < 0 (рис. 22.6, а). Таким образом, полюсы и нули функции Z_LC(s) лежат на мнимой оси и чередуются: 0 £ w₀ < w₁ < w₂ < w₃ < ... Возможный характер зависимости, удовлетворяющий этому соотношению, приведен на рис. 22.6, б.

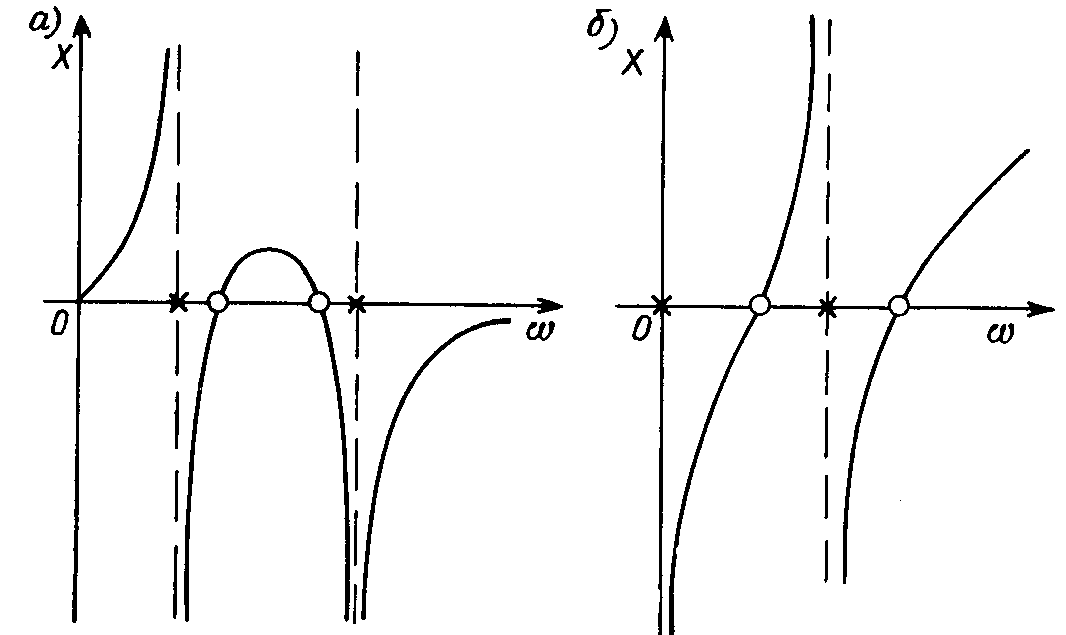
Рис. 22.6

Так как функция , то установленный закон чередования полюсов и нулей относится и к ней, и выражение (22.4) описывает также и входную проводимость цепи.

Еще одно важное свойство входных функций F_LC(s) связано с вычетами в полюсах этих функций. В окрестности полюса s_0i = jw_i характер F(s) определяется соответствующим данному полюсу членом разложения ее на простейшие дроби k_i/(s – jw_i). Если предположить, что вычет k_i — комплексный, т. е. k_i = k_i' + jk_i", то вещественная часть дроби

в правой полуплоскости при s > 0 может стать отрицательной. Действительно, значения s > 0 и w можно выбрать такими, чтобы числитель последней дроби был отрицательным. Следовательно, и сама функция F_LС(s) будет иметь при этом отрицательную вещественную часть. Однако это противоречит условию положительности (22.3) входных функций и поэтому невозможно. Таким образом, k_i" = 0, а s ³ 0, т. е. все вычеты функции F_LC(s) вещественны и положительны.