25.1. УРАВНЕНИЯ ЛИНИИ С РАСПРЕДЕЛЕННЫМИ ПАРАМЕТРАМИ, ИХ РЕШЕНИЕ В СИНУСОИДАЛЬНОМ РЕЖИМЕ
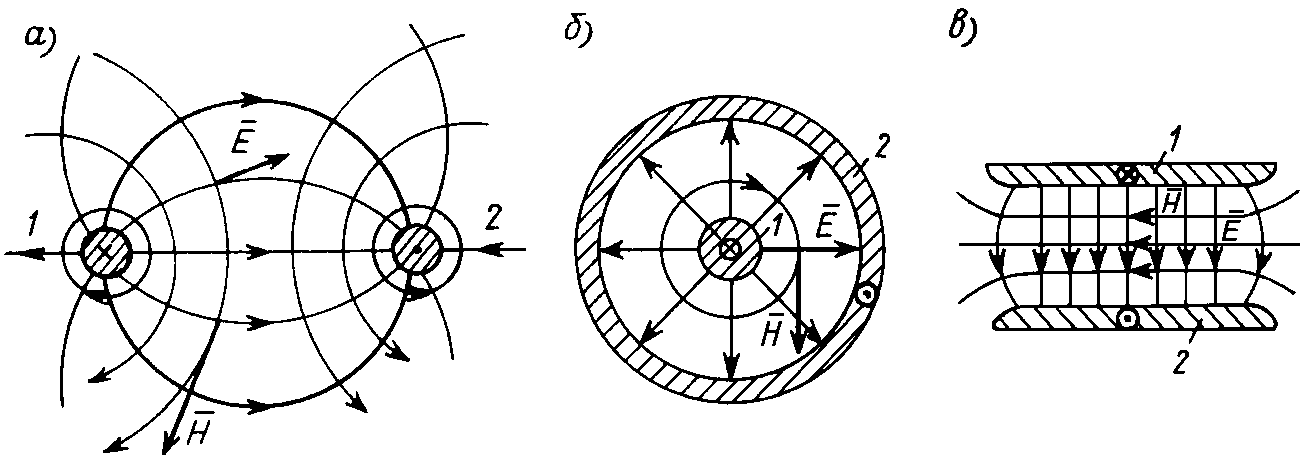
Во всех предыдущих разделах курса мы рассматривали цепи с сосредоточенными параметрами, для которых можно было считать выполненным допущение о том, что наблюдаемые в них физические явления (накопление энергии в электрическом и магнитном полях, выделение тепла или совершение механической работы) связаны с отдельными участками цепи — емкостями, индуктивностями и сопротивлениями. В реальных электромагнитных устройствах это допущение никогда не выполняется, так как процессы, протекающие в каждом отдельном элементе цепи — конденсаторе, катушке и резисторе — имеют различную физическую природу. Так, накопление энергии в электрическом поле конденсатора сопровождается выделением тепла в диэлектрике, разделяющем его обкладки, и т.п. Поэтому любой реальный элемент всегда представляет систему с распределенными параметрами, в которой все перечисленные процессы протекают совместно. Однако наиболее заметно это проявляется в элементах цепи, протяженных вдоль какой-либо координаты. Одним из таких характерных элементов является линия. Независимо от конструктивного выполнения, для воздушной (поперечное сечение которой изображено на рис. 25.1, а), коаксиальной (рис. 25.1, б), полосковой (рис. 25.1, в) линий в пространстве между проводами 1 и 2 с прямым и обратным током накапливается энергия в электрическом и магнитном полях, выделяется тепло как в проводах, обтекаемых током, так и в разделяющем их диэлектрике.
Рис. 25.1
Интенсивность этих явлений характеризуется распределенными параметрами линии — емкостью C, индуктивностью L, сопротивлением R и проводимостью утечки G, отнесенными к длине линии. Для упрощения записи будем обозначать их теми же символами C, L, R, G, что и ранее для сосредоточенных параметров. При этом размерность учитывает их распределенный характер (C — Ф/км; L — Гн/км и т. д.). Параметры R и G не связаны между собой, так как они описывают различные физические процессы: R — выделение тепла в проводах, G — тепловыделение в диэлектрике между проводами, обусловленное токами утечки.
В цепях с распределенными параметрами мы наблюдаем качественно новые закономерности передачи сигналов, например, конечную скорость их распространения — эффект, не учитываемый в теории цепей с сосредоточенными параметрами.
Будем описывать процессы в линии (рис. 25.2) с помощью напряжения и тока u(x, t), i(x, t), являющихся функциями двух переменных — пространственной координаты х и времени t. Таким образом, задача анализа электрических цепей с распределенными параметрами в математическом отношении является более сложной, так как в общем случае происходящие в них процессы описываются дифференциальными уравнениями в частных производных.
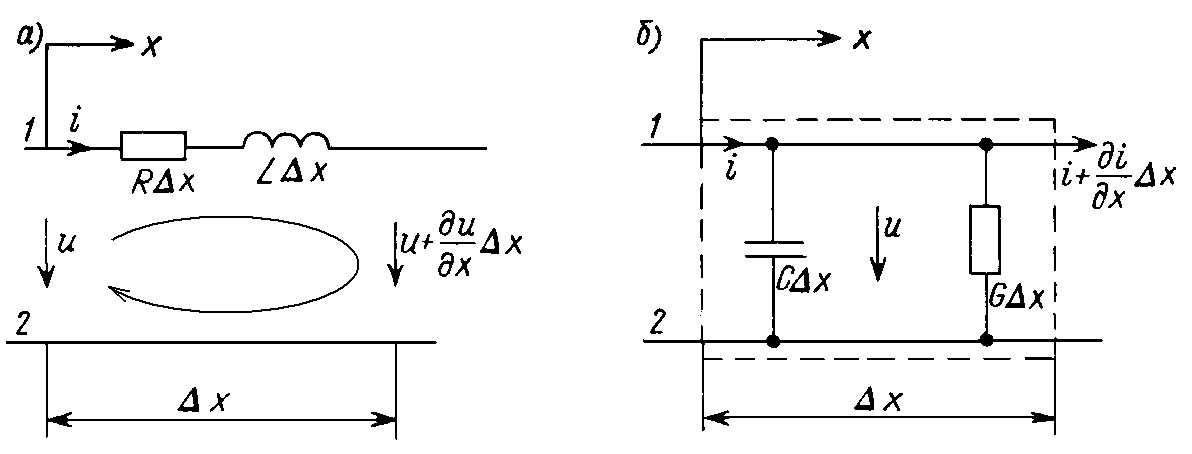
Рис. 25.2
Для получения этих уравнений рассмотрим отрезок линии длиной Dx. Принимая направление отсчета тока в проводе 1, совпадающим с направлением отсчета координаты x, а направление отсчета напряжения от этого провода к проводу 2, запишем на основании второго закона Кирхгофа для контура, изображенного на рис. 25.2, а:
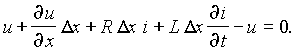
После сокращения и деления на Dx, получим уравнение – ¶u/¶x = Ri + L ¶i/¶t. Рассматривая баланс токов в смежных сечениях линии (рис. 25.2, б), запишем на основании первого закона Кирхгофа
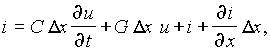
из которого после аналогичных преобразований следует – ¶i/¶x = Gu + C ¶u/¶t. Оба выведенных уравнения:
|
|
являются основными в теории цепей с распределенными параметрами и называются уравнениями линии (телеграфными уравнениями). Линия, параметры которой R, G, C, L постоянны по длине, называется однородной.
Для анализа режима работы линии, когда токи и напряжения во всех точках изменяются во времени по синусоидальному закону, воспользуемся комплексным методом — перейдем от мгновенных величин
u(x, t), i(x, t) к комплексным
, 
. Так как напряжение
зависит только от х, то для комплексных тока и напряжения получаем обыкновенные дифференциальные уравнения:
Для их решения исключим из обоих уравнений ток
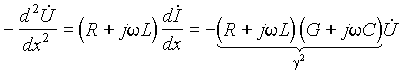
и получим
где
.
Общее решение последнего уравнения запишем в двух формах — через экспоненциальные и гиперболические функции:
Из системы комплексных уравнений нетрудно найти для тока
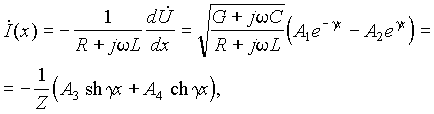
где обозначено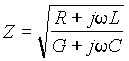 
.
Величина
называется коэффициентом распространения, а
Z – волновым сопротивлением линии; g = a + jb (a — коэффициент затухания,
b — коэффициент фазы). Размерность
g — 1/км, Z — Ом.
Запишем решения уравнений линии при заданных напряжении и токе в начале линии при
x = 0: 
; 
.
При этом удобнее использовать
гиперболические функции в решении. Имеем
A3 = 
, A4 = 
, поэтому
Для напряжения 
и тока 
на конце линии (при
x = l) получим:
Эти соотношения можно разрешить относительно входных величин:
Последние уравнения совпадают с уравнениями симметричного четырехполюсника (см. п.12.8). Поэтому линия представляет собой симметричный четырехполюсник, имеющий меру передачи g = gl и характеристическое сопротивление, равное волновому, Zc = Z. Из последних уравнений легко также определить А параметры четырехполюсника, эквивалентного линии.
Пример определения параметров линии в установившемся синусоидальном режиме приведен в задаче 23.1.
