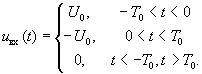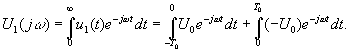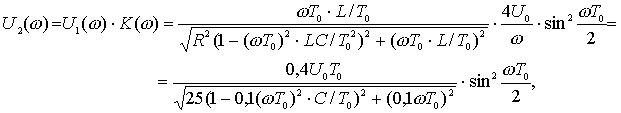Тема 10. РАСЧЕТ ЦЕПЕЙ ПРИ ДЕЙСТВИИ НЕСИНУСОИДАЛЬНОГО СИГНАЛА ЧАСТОТНЫМ МЕТОДОМ
(задачи с решением)
Перейти к задачам без решения
|
Задача 10.1. На входе цепи действует периодическая последовательность треугольных импульсов напряжения (один
из которых изображен на рис. П10.1,
а).
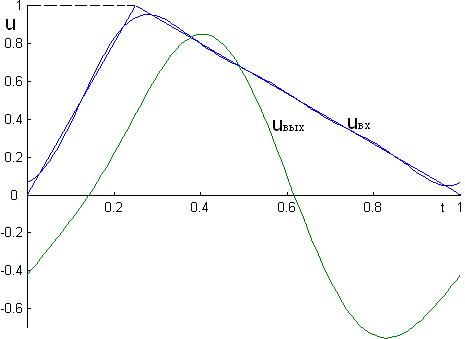
Рис. П10.1, a
Сопротивления элементов для первой гармоники указаны на схеме цепи в омах (рис.П10.1,
б).

Рис. П10.1, б
Разложить входное напряжение в ряд Фурье (см. п. 11.1 теоретического материала) и изобразить его амплитудный спектр. Ограничиваясь при расчете гармониками, амплитуда которых превышает 5% от амплитуды максимальной гармоники, рассчитать и построить спектр выходного напряжения и график его мгновенного значения. Определить действующие значения входного и выходного напряжений. Оценить влияние отброшенных гармоник на действующее значение входного напряжения.
|
Напряжение, действующее на входе цепи, описываемое зависимостью
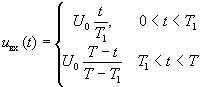 ,
,
представим в виде ряда Фурье
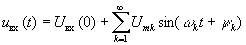 , где
ωk = 2πk/T — угловая частота
k-ой гармоники.
, где
ωk = 2πk/T — угловая частота
k-ой гармоники.
Постоянную составляющую входного напряжения
Uвх(0) найдем непосредственным интегрированием
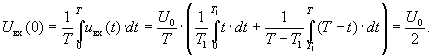
Для упрощения вычисления остальных комплексных коэффициентов ряда Фурье входного напряжения
 , требующего интегрирования по частям, воспользуемся выражением для Фурье-изображения производной
, требующего интегрирования по частям, воспользуемся выражением для Фурье-изображения производной
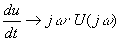 . Поскольку производная входного напряжения представляет кусочно-постоянную функцию
. Поскольку производная входного напряжения представляет кусочно-постоянную функцию
 ,
,
то для ее Фурье-изображения имеем
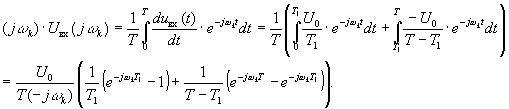
Учитывая, что 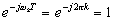 и перенося множитель jωk в правую часть, приведем выражение для искомых коэффициентов к виду
и перенося множитель jωk в правую часть, приведем выражение для искомых коэффициентов к виду
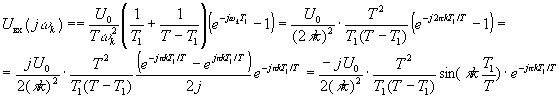
Поскольку амплитуды гармоник входного напряжения
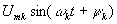 равны удвоенному модулю комплексного коэффициента ряда Фурье, а его аргумент равен начальной фазе
ψk – π/2, то для искомых характеристик входного напряжения получим окончательно:
равны удвоенному модулю комплексного коэффициента ряда Фурье, а его аргумент равен начальной фазе
ψk – π/2, то для искомых характеристик входного напряжения получим окончательно:

Результаты вычисления амплитуд Umkвх и начальных фаз
ψkвх первых восьми гармоник, приведенные в Таблице для
T1/T = 0,25, показывают, что амплитуда гармоник с
k > 4 составляет менее 5% от амплитуды первой гармоники, и поставленное условие позволяет ими пренебречь.
Таблица
|
k |
Umkвх/U0 |
ψkвх,° |
K(ωk) |
θ,° |
Umkвых/U0 |
ψkвых,° |
ψkвых, рад. |
|
0 |
0,5000 |
– |
0 |
– |
0 |
– |
– |
|
1 |
0,3821 |
– 45 |
2,0000 |
0 |
0,7642 |
– 45 |
– 0,7854 |
|
2 |
0,1351 |
– 90 |
0,8944 |
207 |
0,1208 |
117 |
2,0344 |
|
3 |
0,0425 |
– 135 |
0,2769 |
194 |
0,0118 |
59 |
1,0341 |
|
4 |
0 |
– |
– |
– |
0 |
– |
– |
|
5 |
0,0153 |
– 45 |
0,0861 |
188 |
0,0013 |
143 |
2,4958 |
|
6 |
0,0150 |
– 90 |
0,0584 |
187 |
0,0009 |
97 |
1,6930 |
|
7 |
0,0078 |
– 135 |
0,0424 |
184 |
0,0003 |
49 |
0,8552 |
|
8 |
0 |
– |
– |
– |
0 |
– |
– |
Оценим влияние числа учитываемых гармоник на действующее значение входного напряжения. Его точное значение можно найти путем непосредственного интегрирования как
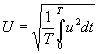 . В результате получим
. В результате получим
 .
.
Вычисление действующего значения через гармонические составляющие сводится к определению корня из суммы квадратов действующих значений отдельных гармоник
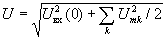 . Применение этой формулы с учетом постоянной составляющей и только первой гармоники дает результат
U = 0,5683U0, что отличается от точного значения на 1,5%. Дополнительный учет второй гармоники дает
U = 0,5763U0, а при учете трех гармоник получим
U = 0,5771U0.
. Применение этой формулы с учетом постоянной составляющей и только первой гармоники дает результат
U = 0,5683U0, что отличается от точного значения на 1,5%. Дополнительный учет второй гармоники дает
U = 0,5763U0, а при учете трех гармоник получим
U = 0,5771U0.
Далее для нахождения спектра выходного сигнала определим передаточную функцию цепи
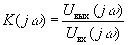 . Используя выражение для входного сопротивления цепи
. Используя выражение для входного сопротивления цепи
 , найдем сначала входной ток
, найдем сначала входной ток
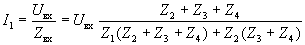 , а затем, используя правило деления тока в параллельных ветвях, получим выражение для тока в выходной ветви
, а затем, используя правило деления тока в параллельных ветвях, получим выражение для тока в выходной ветви
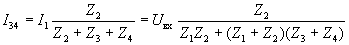 ,
,
которое приводит к выражению для выходного напряжения
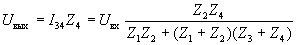 .
.
Таким образом, передаточная функция рассматриваемой цепи имеет вид дроби
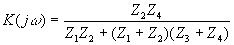 .
.
Используя выражения комплексных сопротивлений элементов цепи для
k-ой гармоники  , представим передаточную функцию в числовом виде
, представим передаточную функцию в числовом виде
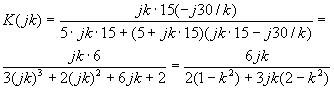 .
.
Численные значения модуля K(ωk)
и аргумента θ передаточной функции для гармоник с
k = 1–7 представлены в Таблице. Поскольку
K(0) = 0, то постоянная составляющая в спектре выходного напряжения отсутствует. Производить вычисление передаточной функции для гармоник с
k = 4 и 8, которые отсутствуют в спектре входного сигнала, также нет необходимости. Из Таблицы видно, что гармоники с
k = 5 – 7 в спектре выходного сигнала выражены еще слабее, так как сама цепь подавляет высшие гармоники, являясь, по существу, полосовым фильтром. Таким образом, для выходного напряжения цепи запишем окончательно, учитывая лишь первую, вторую и третью гармоники:
 , где ω = 2π/T — круговая частота первой гармоники.
, где ω = 2π/T — круговая частота первой гармоники.
Кривая выходного напряжения,
построенная по этому выражению, изображена на рис.П10.1,
а. Здесь же представлен результат суммирования постоянной составляющей и первых трех гармоник входного напряжения. Очевидно, что влияние отброшенных гармоник более высокого порядка на форму кривой входного напряжения весьма невелико и заметно лишь вблизи точек ее излома при
t = 0 и t = T1. Действующее значение выходного напряжения определим по найденным трем гармоникам
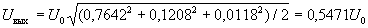 , что весьма близко к действующему значению первой гармоники
, что весьма близко к действующему значению первой гармоники
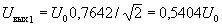 .
.
При работе в режиме изучения теоретического материала вернитесь назад к тексту
Лекции 11.
|
Задача 10.2. Непериодический сигнал, состоящий из двух прямоугольных импульсов напряжения противоположной полярности ±
U0 и одинаковой длительности T0 (рис.П10.2,
а) подается на вход цепи (рис.П10.2, б), параметры которой
L/T0 = 0,1 Ом и R = 5 Ом.

Рис. П10.2, a

Рис. П10.2, б
Определить спектральную плотность входного напряжения и исследовать зависимость спектральной плотности выходного напряжения от величины емкости конденсатора, принимая
C/T0 = 0,1; 0,25 и 1 См.
|
Спектральная плотность входного сигнала, описываемого функцией:
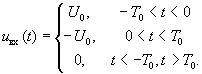
находится с помощью прямого преобразования Фурье:
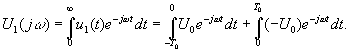
Вычисление интегралов дает:
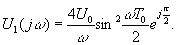
Очевидно, что поскольку исходный сигнал является нечетной функцией, то его спектральная плотность — чисто мнимая величина.
Спектральная плотность выходного сигнала
U2(jw) находится из соотношения
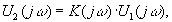
где K(jw) — передаточная функция цепи (рис.П10.2, б) определяется как

где 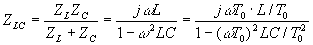 .
.
Поэтому амплитуда спектральной плотности выходного сигнала равна
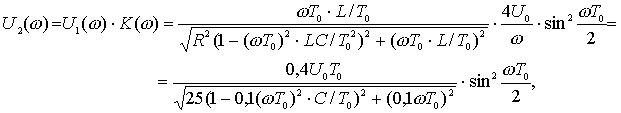
а ее фаза

На рис.П10.3 изображены графики модуля спектральной плотности входного (кривая 1) и выходного напряжений (кривые 2, 3 и 4) для указанных значений емкости в функции безразмерного аргумента
wT0.

Рис. П10.3
Для всех рассмотренных значений емкости существенная часть спектра выходного напряжения ограничена его первыми двумя лепестками. Однако характер спектральной плотности выходного напряжения существенно зависит от величины емкости. При резонансе в цепи модуль передаточной функции достигает максимального значения, равного единице, и на соответствующей частоте спектральные плотности входного и выходного напряжений равны друг другу. Для
C/T0 = 0,1 См эта частота равна
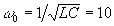 . На частотах, удаленных от резонансной, спектральная плотность выходного напряжения существенно меньше, чем входного: рассматриваемая цепь представляет собой полосовой фильтр. При
C/T0 = 0,25 См резонансная частота
ω0 » 6,3, что практически совпадает с
ω = 2π, при которой спектральная плотность
U1(ω) = 0. Поэтому на этой частоте и
U2(ω) = 0. При C/T0 = 1 См
ω0 » 3,16, и зависимость U2(ω) имеет на этой частоте резкий всплеск; остальные же частотные составляющие спектра подавлены. Это означает, что при этом значении емкости временная зависимость
u2(t) близка к синусоиде с частотой
ω0.
. На частотах, удаленных от резонансной, спектральная плотность выходного напряжения существенно меньше, чем входного: рассматриваемая цепь представляет собой полосовой фильтр. При
C/T0 = 0,25 См резонансная частота
ω0 » 6,3, что практически совпадает с
ω = 2π, при которой спектральная плотность
U1(ω) = 0. Поэтому на этой частоте и
U2(ω) = 0. При C/T0 = 1 См
ω0 » 3,16, и зависимость U2(ω) имеет на этой частоте резкий всплеск; остальные же частотные составляющие спектра подавлены. Это означает, что при этом значении емкости временная зависимость
u2(t) близка к синусоиде с частотой
ω0.
При работе в режиме изучения теоретического материала вернитесь назад к тексту Лекции 11.
Конец
Обратно к списку тем практических занятий
Обратно к плану соответствующей лекции


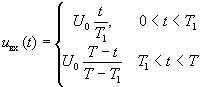 ,
,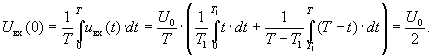
 , требующего интегрирования по частям, воспользуемся выражением для
, требующего интегрирования по частям, воспользуемся выражением для  ,
,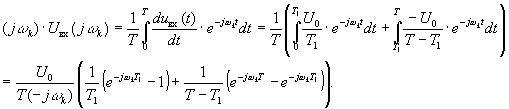
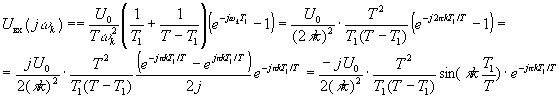
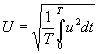 . В результате получим
. В результате получим
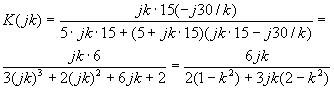 .
.