19.2. ПРЕОБРАЗОВАНИЕ ЛАПЛАСА, ЕГО ОСНОВНЫЕ СВОЙСТВА. ИЗОБРАЖЕНИЕ ФУНКЦИЙ
Преобразование Лапласа, связывающее функцию времени f(t) — оригинал и ее операторное изображение F(s) —
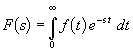
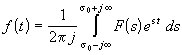
является весьма развитым инструментом математического анализа и ему посвящена обширная литература. Многие его свойства идентичны свойствам преобразования Фурье, рассмотренным в п. 11.3. Остановимся на тех из них, которые будут использоваться при расчете переходных процессов операторным методом.
Линейность преобразования Лапласа. Так как формула прямого преобразования линейна относительно подынтегрального сомножителя f(t), то преобразование линейно — изображение суммы оригиналов 
равно сумме изображений слагаемых
.
Изображение простейших функций времени. Так как преобразование является односторонним, то все рассматриваемые функции определены своими выражениями лишь при t > 0, а при t < 0 их значения равны нулю. Поэтому при нахождении изображения экспоненты f(t) = e–at необходимо учитывать, что речь идет о функции, изображенной на рис. 19.2, а.
a)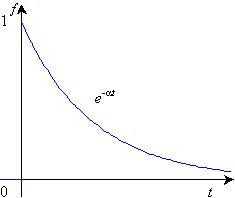
б)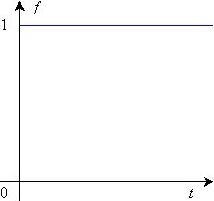
Рис. 19.2
Непосредственное применение интеграла прямого преобразования дает
.
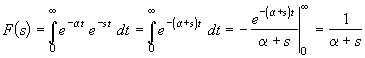(На верхнем пределе экспонента исчезает, так как Re(s) = s > 0). Это — единственная из множества формул преобразования Лапласа функций, которую полезно запомнить.
Полученный результат
приводит к изображению единичной функции f(t) = 1(t) (рис.
19.2, б). Найдем его, принимая в формулах для экспоненты
a = 0. Таким образом, 1(t) имеет изображение
1/s. По основной формуле преобразования изображение
d–функции 
. Действительно, подынтегральная функция отлична от нуля лишь при t = 0, когда экспонента равна единице, а 
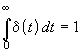по определению. Отсюда следует, в частности, что нижний предел в интеграле Лапласа следует принимать равным (– 0), что существенно лишь для функций, неограниченных в начальный момент времени — содержащих слагаемое
d(t). Обозначим соответствие оригинала и изображения в символической форме
f(t) ®
F(s).
Имеем
; 
; 
.
Наиболее часто встречающиеся изображения других функций приведены в Приложении 4. Значительное число изображений других функций можно найти в Л.16. Расширить перечень указанных функций можно с помощью теоремы смещения, согласно которой изображение функции f(t), умноженной на экспоненту e–at, равно F(s + a):
e–atf(t) ® F(s + a).
Изображение производной функции. Изображение
F'(s) производной функции f'(t) = df/dt выражается через изображение дифференцируемой функции с помощью основного интеграла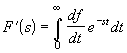 
. Применяя интегрирование по частям, перепишем его в виде
.
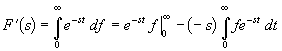Поскольку последний интеграл представляет собой изображение исходной функции, то после преобразования и подстановки пределов интегрирования приведем полученное соотношение к виду
 .
|
(19.4) |
Предельные соотношения. Используя в формуле (19.4) значение
f(+ 0), перейдем в ней к пределу при s ® ¥. Учитывая, что производная
df/dt при t > 0 ограничена и, следовательно,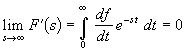 
, получим
.
Рассуждая аналогично, получим также и соотношение
,
дающее возможность определить предельное значение оригинала при t ® ¥ по его изображению, однако, лишь в том случае, если этот оригинал имеет предел при t ® ¥ (например, его нельзя применять к синусоиде).
Теорема запаздывания определяет связь изображения F1(s) функции f1(t) с изображением той же функции, задержанной на время t; f2(t) = f1(t – t) (рис. 19.3, а,б).
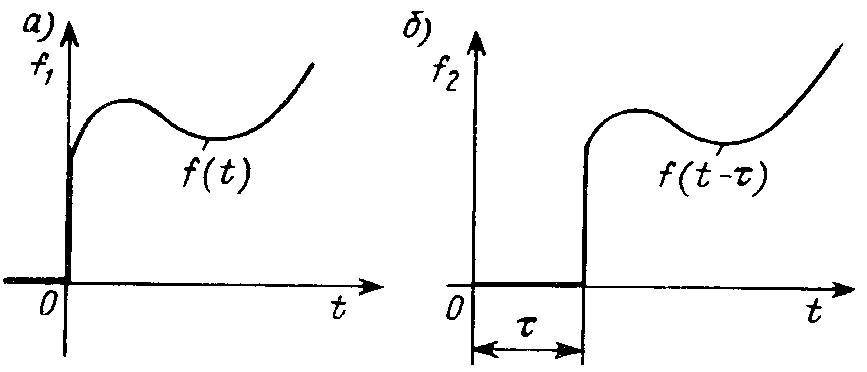
Рис. 19.3
Для F2(s) имеем
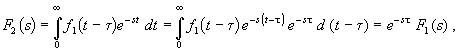
т. е. изображение запаздывающей функции равно изображению исходной функции, умноженной на e–st.
В справочной литературе [Л.16] можно найти описание других свойств преобразования Лапласа.
Отметим, что применяя это преобразование к функциям времени, имеющим размерность, необходимо помнить, что размерности оригинала f(t) и его изображения F(s) не совпадают, — в формуле прямого преобразования интеграл вычисляется по времени, поэтому размерность изображения есть размерность оригинала, умноженная на время. Комплексная переменная s = s + jw, которую иногда называют комплексной частотой, хотя такое название и лишено физического смысла, имеет размерность частоты (1/с).
