20.2. ВРЕМЕННОЙ МЕТОД РАСЧЕТА ПЕРЕХОДНЫХ ПРОЦЕССОВ. ИНТЕГРАЛ СВЕРТКИ. ИНТЕГРАЛ ДЮАМЕЛЯ
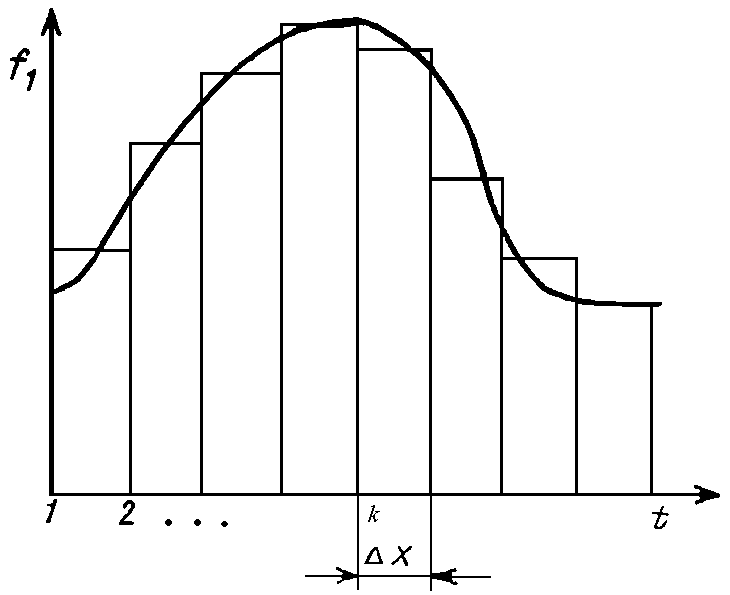
Рассмотрим процесс в цепи при действии на ее входе сигнала произвольной формы f1(t) (рис. 20.3). Этот сигнал можно представить в виде последовательности прямоугольных импульсов длительностью Dx с амплитудами f1(kDx).
Рис. 20.3
При малых значениях Dx каждый такой импульс эквивалентен действию на цепь
d-импульса, включаемого в момент
t = kDx и имеющего площадь
f1(kDx) Dx. Поэтому входной сигнал представим в виде суммы
. После перехода к пределу при
Dx ®
0, kDx ®
x получим 
.
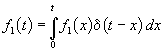Поскольку реакция цепи на каждый d-импульс описывается импульсной характеристикой hd, то для выходной величины f2(t) можно записать аналогичный интеграл, в котором реакция на входной импульс d(t – x) выражена как hd(t – x):
.
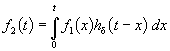Полученный интеграл называется интегралом свертки и используется при вычислении реакции цепи f2(t) на воздействие f1(t) произвольной формы. Он и является основой временнóго метода расчета переходных процессов.
Как уже отмечалось, указанные выше пределы интегрирования требуют уточнения, особенно, при наличии в подынтегральных сомножителях слагаемых в виде d-функций. При вычислении интеграла свертки необходимо учитывать, что первый сомножитель под интегралом f1(x) = 0 при x < – 0; соответственно hd(t – x) = 0 при t – x < – 0, то есть при x > t + 0. Именно эти значения пределов интегрирования (– 0 < x < t < + 0) необходимо рассматривать при вычислении. При ограниченном значении f1 d-слагаемое может содержаться в hd(t – x). Вклад этого слагаемого можно учесть отдельно. Для этого запишем
.
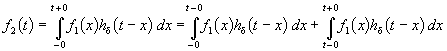Так как второй интеграл можно преобразовать к виду
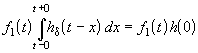, то окончательно получим
.
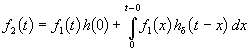В последнем выражении под интегралом учитывается только ограниченная часть импульсной характеристики hd.
Пример использования интеграла свертки рассмотрен в Задаче 17.1.
Основные свойства интеграла свертки.
1. Поскольку при t < 0 обе подынтегральные функции f1(t) и hd(t) º 0, то пределы в интеграле свертки можно взять от - ¥ до ¥, то есть
,
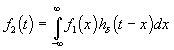так как на добавленных отрезках (– ¥, 0) и (t, ¥) один из подынтегральных сомножителей тождественно равен нулю.
2. Переменные интегрирования можно заменять, используя связь t – x = y. Интеграл при этом примет вид
.
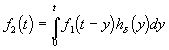Операция свертки растягивает импульсный сигнал во времени. Пусть прямоугольный импульс A длительностью T (рис. 20.4, а) действует на входе цепи, импульсная характеристика которой изображена на рис. 20.4, б. Такая цепь представляет интегратор с конечным временем интегрирования t.
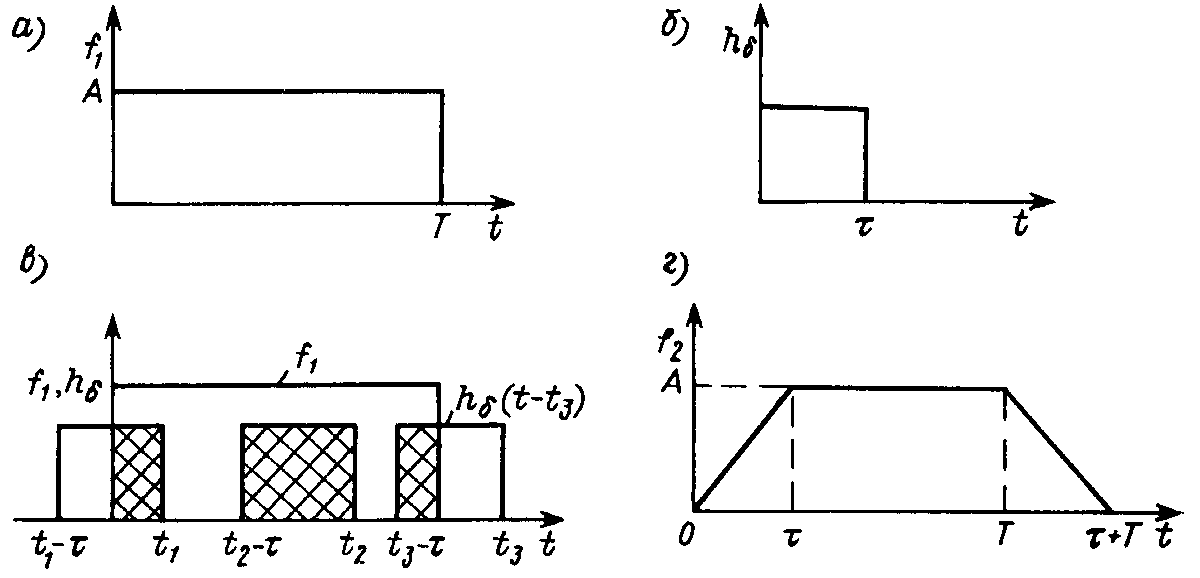
Рис. 20.4
В этом простом случае результат свертки легко найти графически. Пусть для определенности T > t, тогда для различных моментов времени t1, t2 и t3 произведение f1 на h(t – x) будет определяться площадью перекрывающихся прямоугольников (рис. 20.4, в), и выходной сигнал будет иметь вид, показанный на рис. 20.4, г. Таким образом, цепь суммирует длительность импульса T и собственное время t.
Интеграл Дюамеля. Интеграл свертки можно выразить через переходную характеристику. Это приводит к интегралу Дюамеля. Для его получения используем записанную п. 20.1 связь hd = dh/dt, из которой произведение hd(t – x) dx можно представить как – dh(t – x):
.
В последнем преобразовании использована формула интегрирования по частям. Так как внеинтегральный член равен нулю, то окончательно получим
,
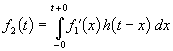где 
.
Неудобство этого выражения связано с
d-слагаемыми в 
, которые появляются, если входной сигнал
f1(t) имеет разрывы. При наличии разрыва в точке
t = 0 [f1(– 0) = 0, f1(+ 0) ¹
0],] его можно выделить и записать
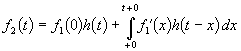
Последнее выражение является наиболее распространенной формой записи интеграла Дюамеля.
Если входная функция f1 имеет разрывы, то для расчета переходного процесса временным методом удобнее использовать интеграл свертки, если она непрерывна, то — интеграл Дюамеля (при неограниченной характеристике hd).
При выполнении расчетов временным методом следует обращать внимание на: 1) различное аналитическое описание функции f1 на различных отрезках у импульсов сложной формы; 2) правильный учет неограниченного характера функции hd (при вычислении интегралов с d-слагаемыми); 3) правильный учет разрывов функции f1 в интеграле Дюамеля.
Пример расчета переходного процесса с помощью интеграла Дюамеля рассмотрен в Задачe 17.2.
Особенности применения операторного метода при определении «последействия» импульса. Реакция цепи на одиночный импульс длительностью Т при t > Т содержит лишь свободные составляющие процесса, соответствующие корням характеристического уравнения цепи. В связи с этим при использовании операторного метода нахождение оригинала по теореме разложения требует учета не всех корней знаменателя изображения реакции, а лишь тех из них, которые являются корнями знаменателя передаточной функции. Это существенно упрощает расчет, особенно для импульсов сложной формы. Пусть определено изображение импульса с конечной длительностью
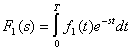
(f1(t) = 0 при t > T). При воздействии такого импульса на цепь с передаточной функцией K(s) = Q(s)/P(s) реакция при t > Т содержит лишь экспоненты еskt с показателями, в которые входят корни P(s) =0. Поэтому для реакции при t > Т по теореме разложения имеем
(предполагается отсутствие кратных корней sk).
Рассмотрим в качестве примера Задачу 17.1. Передаточная функция цепи имеет выражение K(s) = st/(l + st). Операторное изображение входного сигнала имеет вид
Поэтому изображение выходного напряжения равно
а само напряжение u2(t) —
что совпадает с результатом, полученным в Задаче 17.1.
Если воздействующий импульс f1(t) не имеет простого аналитического описания, то его представляют в виде совокупности импульсов прямоугольной формы с амплитудой f1(tk) длительностью Dtk, каждый из которых рассматривается как d-импульс
(рис. 20.5)
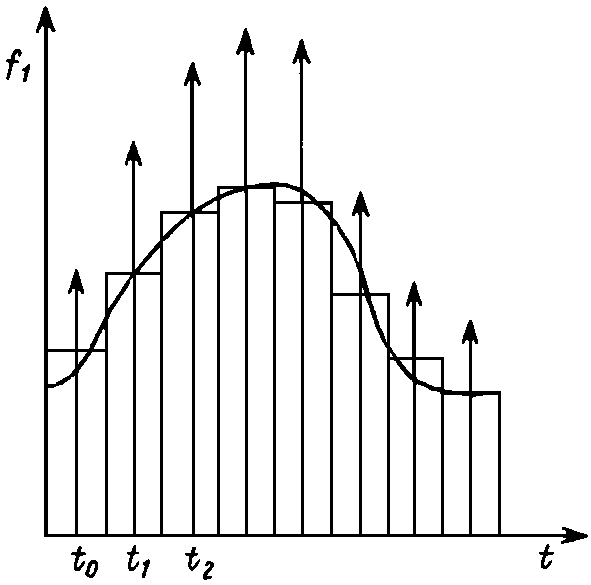
Рис. 20.5
С помощью теоремы запаздывания получим изображение входного сигнала F1(s)
При таком представлении временной метод приводит к замене интеграла свертки суммой; для выходного сигнала будем иметь
.
