Задача 17.1. На входе цепи, изображенной на рис. П17.1, a, действует импульс u1(t) длительностью T (рис.П17.1, б)
а) 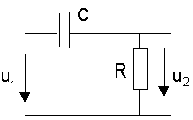 |
б)   |
Рис. П17.1.
Определить зависимость u2(t).
Тема 17. ИНТЕГРАЛ СВЕРТКИ И ИНТЕГРАЛ ДЮАМЕЛЯ
(задачи с решением)
Перейти к задачам без решения
|
Задача 17.1. На входе цепи, изображенной на рис. П17.1, a, действует импульс u1(t) длительностью T (рис.П17.1, б)
Рис. П17.1. Определить зависимость u2(t). |
Выражение для импульсной характеристики цепи было определено в
п. 20.1: ![]() .
Поскольку входной сигнал имеет различные выражения на отдельных интервалах времени
0 < t < T и T < t < ¥, интеграл свертки записывается для этих интервалов по-разному:
.
Поскольку входной сигнал имеет различные выражения на отдельных интервалах времени
0 < t < T и T < t < ¥, интеграл свертки записывается для этих интервалов по-разному:
1) при ![]()


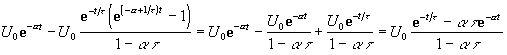 ;
;
2) при ![]()
 .
.
Интеграл от слагаемого с d-функцией во втором случае пропадает, так как на промежутке интегрирования аргумент d-функции нигде не обращается в нуль. Поэтому для выходного сигнала на этом интервале получим выражение
 ,
,
которое определяет отрицательное значение
![]() независимо от значения параметра at
— после прекращения действия входного импульса выходное напряжение изменит знак на противоположный.
независимо от значения параметра at
— после прекращения действия входного импульса выходное напряжение изменит знак на противоположный.
При работе в режиме изучения теоретического материала вернитесь назад к тексту Лекции 20.
|
Задача 17.2. Определить зависимость выходного тока i2(t) цепи рис. П16.2, на входе которой действует треугольный импульс тока i1(t) (рис. П17.2).
Pис. П17.2 |
Рассматриваемый импульс описывается линейной зависимостью
![]()
Поэтому решение проще получить с помощью интеграла Дюамеля, поскольку в этом случае при интегрировании используется производная входного тока i1' = I0/T и переходная характеристика цепи
![]() , найденная ранее в Задаче 16.2.
, найденная ранее в Задаче 16.2.
На интервале 0 < t < T выходной ток выражается интегралом

При t > T интеграл 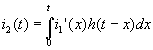 следует представить в виде суммы трех слагаемых, поскольку производная
i1' имеет различное выражение в различных интервалах
следует представить в виде суммы трех слагаемых, поскольку производная
i1' имеет различное выражение в различных интервалах
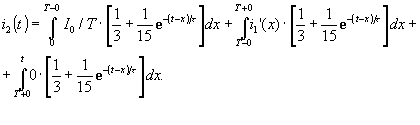
Первых из этих интегралов вычисляется подобно предыдущему и равен
![]()
С учетом того, что сомножитель подинтегральной функции второго интеграла, выражаемый переходной характеристикой, при t = T непрерывен и, следовательно, его можно вынести из-под интеграла, представим этот интеграл в виде
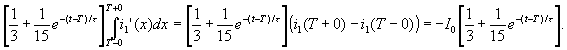
Третий же интеграл равен нулю, так как на интервале T < t < ∞ один из сомножителей подинтегральной функции здесь равен нулю. Суммируя перечисленные выражения слагаемых, получим окончательно для рассматриваемого промежутка
![]()
При работе в режиме изучения теоретического материала вернитесь назад к тексту Лекции 20.