21.4. ЧАСТОТНОЕ ПРЕДСТАВЛЕНИЕ ДИСКРЕТНЫХ СИГНАЛОВ

Связь между преобразованиями Лапласа и Фурье можно установить и для дискретных сигналов, описываемых решетчатыми функциями f[k]. Заменяя комплексную переменную s на частотную переменную jw, перейдем к преобразованию Фурье дискретных сигналов, позволяющему вести их анализ в частотной области. Напомним соответствие между односторонними преобразованиями Лапласа непрерывных и дискретных сигналов (табл. 21.1).

Таблица 21.1

ПРЕОБРАЗОВАНИЕ ЛАПЛАСА

Спектральное представление непериодических сигналов. Для перехода к преобразованию Фурье решетчатых функций, которые теперь будем считать заданными на неограниченном интервале дискретного аргумента – ¥  < k < ¥, осуществим в дискретном преобразовании Лапласа указанную замену частотной переменной s ® jw и соответствующие замены пределов суммирования и интегрирования. В результате получим формулы двустороннего преобразования Фурье решетчатых функций:

Таблица 21.2

ПРЕОБРАЗОВАНИЕ ФУРЬЕ

Как и формулы преобразования Фурье непрерывного сигнала, полученные соотношения выражают дискретный сигнал в виде совокупности бесконечного числа дискретных гармонических составляющих с бесконечно малыми амплитудами, спектральная плотность которых теперь ограничена интервалом изменения частоты от - p/T до p/T. За пределами этого интервала спектральная плотность дискретного сигнала F(jw)  является периодической функцией частоты с периодом w₀ = 2p/T: значения спектральной плотности при аргументе w + nw₀ равны ее значениям при w. Отдельные дискретные гармоники спектра решетчатой функции f[k] представляют собой выборку с шагом дискретизации T синусоидальной функции, имеющей период T_w = Tw₀ /w. Для ряда характерных частот w/w₀, указанных на рисунке, они изображены на рис. 21.3.

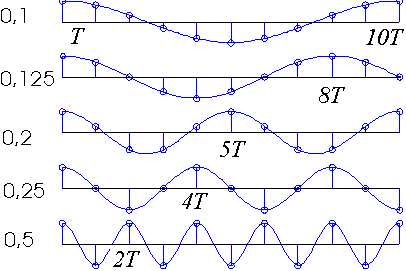
Рис. 21.3

Гармонические составляющие спектра дискретного сигнала с частотами, лежащими за пределами интервала (0, w₀/2), тождественны соответствующим составляющим из этого интервала: например, гармоника с частотой w'< w₀ совпадает с гармоникой частоты w₀ -  w' (см. рис. 21.4).

Рис. 21.4

Поскольку для вещественных f[k] модуль и вещественная часть F(jw) — четные, а мнимая часть и аргумент — нечетные функции частоты, то вся существенная часть информации о спектре дискретного сигнала заключена в диапазоне частот (0, w₀/2). Полученные соотношения могут быть приведены к безразмерному частотному аргументу w/w₀ = wT/2p. В отличие от спектральной плотности F(jw) непрерывного сигнала f(t), которая имеет размерность самого сигнала, умноженную на время, плотность F(jw) решетчатой функции f[k] имеет ту же размерность, что и f[k].

Значительная часть свойств преобразования Фурье непрерывных функций сохраняется и для функций дискретного аргумента (связь вещественной и мнимой частей с четностью функции, свойства линейности и дуальности).

Пример 1. Получим спектральное представление решетчатой функции

,

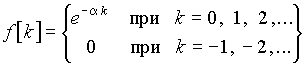для которой ранее было найдено z-изображение F(z) = z/(z – e^–a). Заменяя z = e^jwT, приведем выражение спектральной плотности к виду

.

График модуля ½F(jw)½  = F(w) изображен на рис. 21.5.

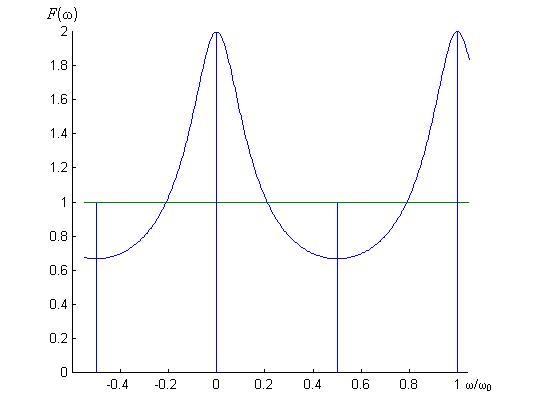
Рис. 21.5

В диапазоне 0 < w/w₀ < 1/2 он монотонно убывает от максимального значения F(0) = 1/(1 – e^–a) до минимума F(w₀/2) = 1/(1 + e^–a).

Пример 2. Спектр ограниченной последовательности, включающей N одинаковых отсчетов, расположенных симметрично относительно начала координат (рис. 21.6, а), описываемой зависимостью

,

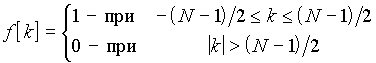выражается геометрической прогрессией с ограниченным числом членов:

.

.

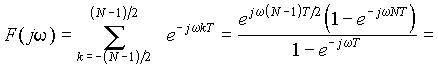
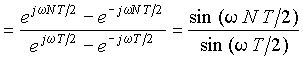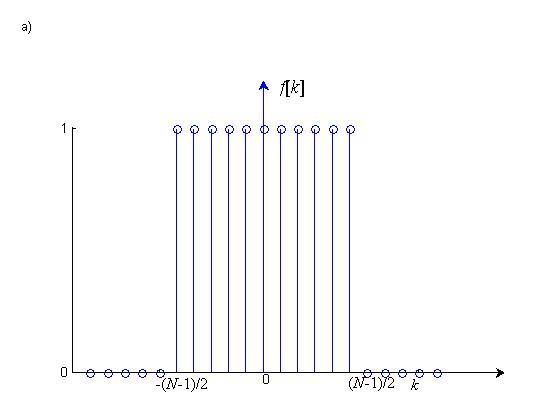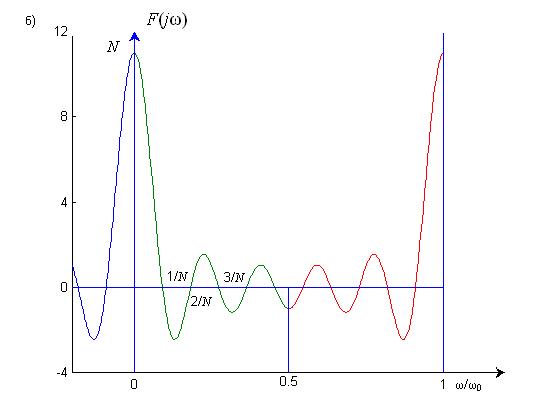
Рис. 2

График ее изображен на рис. 21.6, б.

Еще один пример определения спектра дискретного сигнала рассмотрен в Задаче 19.4.

Спектральное представление периодических сигналов. Периодический дискретный сигнал имеет дискретный периодический спектр, который характеризуется ограниченным числом гармонических составляющих. Если периодическая решетчатая функция, обладающая свойством f[k + N] = f[k], определена N значениями на периоде f[k] = f[0], f[1], ... , f[N – 1], ее спектр описывается решетчатой функцией F[jт], т = 0, ... , N – 1, так как для большего числа гармоник мы не имеем информации.

Для получения выражений для коэффициентов комплексного ряда Фурье периодической решетчатой функции воспользуемся формулами комплексного ряда Фурье непрерывной функции с периодом Т₀ = NТ (Т – шаг дискретизации)

Заменим в интеграле от непрерывной функции на произведение f(kT) Dt = f[k]T, где Т — шаг дискретизации, а также преобразуем произведение частоты w_m = 2pm и времени t_k = kT в показателе экспонент w_mt_k = 2pmt_k/T₀ в 2pmkT/(NT) = 2pmk/N. В результате получим выражения дискретного преобразования Фурье:

Комплексные коэффициенты F[jm] определяют конечный спектр периодической решетчатой функции. Основные свойства дискретного преобразования Фурье вытекают из свойств преобразования Фурье периодических непрерывных функций.

Представления о характере преобразований Фурье непрерывных и дискретных функций обобщены в Табл. 21.3.

Таблица 21.3

Пример. Определим спектральные характеристики периодической решетчатой функции, выражаемой периодической последовательностью f [k] = 0, 1, 2, 3, 4, 5, 6, 7, 0,… (N = 8) (рис. 21.7, а).

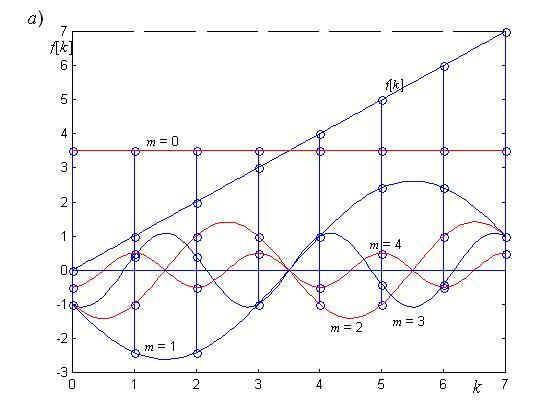
б)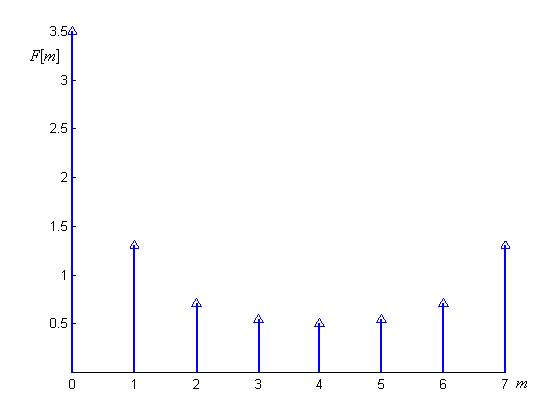

Рис. 21.7

По формуле прямого преобразования имеем:

.

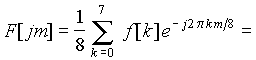
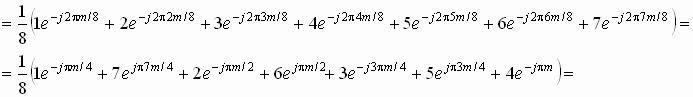
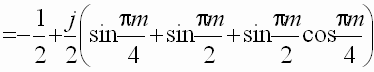При преобразовании последнего выражения использовано соотношение e^jp(8-m)/4 = e^jpm/4 и формула Эйлера. Вычисление комплексных коэффициентов приводит к следующему результату:

F[jm] = 3,5 для m = 0, F[jm] = 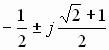 для m = 1,  7, F[jm] = ±1/2 для m = 2, 6, F[jm] = 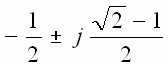 для m = 3,  5, F[jm] = -1/2 для m = 4.

Распределение модулей спектральной характеристики F[т] показано на рис. 21.7, б. Поскольку анализируемый сигнал обладает нечетной симметрией, коэффициенты F[jm] чисто мнимые, и косинусоидальные составляющие в его спектре отсутствуют. Вся существенная информация о спектре содержится в интервале m (0, N/2), что для непериодической решетчатой функции отвечает интервалу частот (0, w₀/2 = p/T).

Пример расчета цепи с помощью дискретного преобразования Фурье рассмотрен в Задаче 19.3.

---

Дальше
Обратно к плану лекции