Тема 19. АНАЛИЗ ИМПУЛЬСНЫХ ПРОЦЕССОВ С ПОМОЩЬЮ
Z-ПРЕОБРАЗОВАНИЯ
(задачи с решением)
Перейти к задачам без решения
|
Задача 19.1. Найти z-изображение периодической последовательности f1[k] = 0, 1, 2, 1, 0, –1, –2, –1, 0, 1, 2,…. и конечной последовательности f2[k] = 0, 1, 2, 1, 0, –1, –2, –1, 0, 0, 0,…. |
Для определения изображения периодической последовательности![]() сгруппируем ее одинаковые члены
f1[k], отличающиеся на период: f1[1], f1[9], f1[17],…; f1[2], f1[10], f1[18],… и т.д.
z-изображение каждой такой группы представляет собой бесконечную геометрическую прогрессию со знаменателем
z –8, поэтому ее сумма равна первому члену, деленному на (1 – z -8). Суммирование всех шести составляющих прогрессий дает
сгруппируем ее одинаковые члены
f1[k], отличающиеся на период: f1[1], f1[9], f1[17],…; f1[2], f1[10], f1[18],… и т.д.
z-изображение каждой такой группы представляет собой бесконечную геометрическую прогрессию со знаменателем
z –8, поэтому ее сумма равна первому члену, деленному на (1 – z -8). Суммирование всех шести составляющих прогрессий дает
![]() .
.
Для конечной последовательности f2[k] результат получим путем непосредственного суммирования
![]() .
.
При работе в режиме изучения теоретического материала вернитесь назад к тексту Лекции 21.
|
Задача 19.2. Найти напряжение на выходе
RC-цепи (рис. 20.1, б), находящейся под действием периодической последовательности идеальных
d-импульсов (рис. П19.1), площади которых равны
Pис. П19.1 |
Для нахождения z-изображения такой последовательности просуммируем отдельно ее четные и нечетные члены:
![]()
![]() .
.
Изображение выходной величины — напряжения на конденсаторе ![]() — получим с помощью найденной в п. 21.3 передаточной функции
— получим с помощью найденной в п. 21.3 передаточной функции
![]() :
:
![]() ,
,
где ![]() .
.
Оригинал ![]() найдем с помощью теоремы о вычетах. Так как знаменатель
найдем с помощью теоремы о вычетах. Так как знаменатель ![]() имеет три простых корня
имеет три простых корня![]() , то формула обратного
z-преобразования дает
, то формула обратного
z-преобразования дает

где ![]() ;
; ![]() .
.
Подставляя значения корней в последнее выражение, получим
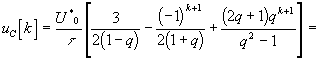
![]() .
.
Первые два слагаемых числителя этой формулы выражают составляющие установившегося периодического процесса, а последнее слагаемое — затухающую составляющую, связанную с переходным процессом при подключении к источнику напряжения.
При работе в режиме изучения теоретического материала вернитесь назад к тексту Лекции 21.
|
Задача 19.3. Решить Задачу 10.1, используя представление периодической последовательности треугольных импульсов входного напряжения с периодом T и передним фронтом T1 решетчатой функцией, имеющей N отсчетов на периоде. |
Общее выражение решетчатой функции, представляющей входное напряжение, имеет вид

где ΔT = T/ N — шаг дискретизации.
Для N = 8 и T1/T = 0,25 имеем uвх[k] = U0(0, 1/2, 1, 5/6, 2/3, 1/2, 1/3, 1/6,…). Применение формулы дискретного преобразования Фурье
![]()
приводит к результату для Uвх[jm]/U0, выражаемому массивом комплексных величин из восьми элементов:
Таблица 19.1
| № элемента | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| m | 0 | 1 | 2 | 3 | 4 | |||
| m – N | – 3 | – 2 | – 1 | |||||
Uвх[jm]/U0 |
0,5 | –0,1423 –0,1423j | –0,0833 | –0,0244 +0,0244j | 0 | –0,0244 –0,0244j | –0,0833 | –0,1423 +0,1423j |
Первый элемент массива с m = 0 представляет постоянную составляющую — нулевую гармонику. Второй и восьмой элементы (m = 1 и m – N = – 1) являются комплексно сопряженными и отвечают первой гармонике. Также комплексно сопряженные третий и седьмой элементы (m = 2 и m – N = – 2) представляют вторую гармонику, четвертый и шестой (m = 3 и m – N = – 3) — третью и, наконец, пятый элемент (m = 4 = N/2) отвечает четвертой гармонике. При четном N он не имеет пары и является вещественным. Таким образом, дискретное преобразование Фурье периодической решетчатой функции, имеющей N отсчетов на периоде, выражает эту функцию как сумму постоянной составляющей и N/2 дискретных гармоник.
Несмотря на то, что для анализа цепи достаточно ограничиться всего тремя гармониками (см. решение задачи 10.1), необходимая точность определения коэффициентов низкого порядка достигается лишь при достаточно больших значениях N. Об этом свидетельствуют значения модуля коэффициентов Фурье первой, второй и третьей гармоник рассматриваемой решетчатой функции, вычисленные при различных N, указанные в следующей таблице.
Таблица 19.2
|
N |
8 |
16 |
32 |
64 |
128 |
256 |
512 |
|
Um1вх/U0 |
0,2012 |
0,1935 |
0,1917 |
0,1912 |
0,1911 |
0,1911 |
0,1911 |
|
Um2вх/U0 |
0,0833 |
0, 0711 |
0,0684 |
0,0678 |
0,0676 |
0,0676 |
0,0676 |
|
Um3вх /U0 |
0,0345 |
0,0239 |
0,0219 |
0,0214 |
0,0213 |
0,0212 |
0,0212 |
Из приведенных данных следует, что необходимая точность определения коэффициентов Фурье непрерывного сигнала при его дискретизации достигается лишь при числе отсчетов на периоде N, имеющем порядок нескольких сот. Поэтому для его реализации используются программы быстрого преобразования Фурье, или по-английски, Fast Fourier Transform (FFT), входящие в состав стандартного математического обеспечения вычислительной техники. Их применение наиболее эффективно при числе отсчетов на периоде N =2n, где n — целое число.
Для определения коэффициентов дискретного ряда Фурье выходного напряжения Uвых[jm], как и в случае непрерывного сигнала, используем передаточную функцию цепи K[jm], и коэффициенты Uвых[jm] находятся как Uвых[jm] = Uвх[jm]·K[jm]. При этом используем выражение передаточной функции рассматриваемой цепи, полученное в задаче 10.1
![]() .
.
На этом этапе расчета алгоритмически наиболее просто использовать всю совокупность элементов Uвх[jm] (m = 0, 1,…, N). При этом в выражение передаточной функции в качестве номера гармоники k для начальной части спектра подставляем значения m = 0, 1,…, N/2, и значения m – N = – N/2 + 1, – N/2 + 2,…, – 1 — для его заключительной части. В результате получим массив N комплексных величин Uвых[jm], имеющей почти ту же симметрию, что и Uвх[jm]: его элементы с индексами m и m – N — комплексно сопряженные; отличие состоит лишь в том, что при комплексном Uвых[jN/2] = Uвх[jN/2]·K[jN/2] ≠ 0 элемент с m = N/2 будет также комплексным.
Решение завершается применением процедуры обратного дискретного преобразования Фурье (Inverse Fast Fourier Transform — IFFT) к массиву Uвых[jm]
![]() ,
,
которое при комплексном Uвых[jN/2] приводит к комплексному результату. Однако при больших N мнимые части невелики, и значения решетчатой функции uвых[k] с достаточной точностью определяются вещественными частями обратного преобразования Фурье.
При работе в режиме изучения теоретического материала вернитесь назад к тексту Лекции 21.
|
Задача 19.4. Определить спектральную плотность непериодического дискретного сигнала, состоящего из двух прямоугольных импульсов напряжения противоположной полярности ± U0 и одинаковой длительности, каждый из которых включает N отсчетов, следующих друг за другом с шагом T (рис.П19.2).
Pис. П19.2 Исследовать зависимость спектральной плотности входного напряжения от числа отсчетов N и сравнить ее со спектральной плотностью аналогичного непрерывного сигнала, рассмотренного в Задаче 10.2. |
Входной сигнал выражается решетчатой функцией

Применение формулы прямого Фурье-преобразования дискретного сигнала дает:
![]() .
.
Суммирование геометрических прогрессий и переход от экспонент с комплексными показателями к тригонометрическим функциям приводит к результату:
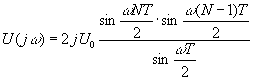 .
.
Предельный переход при N → ∞, T → 0 и NT = T0 = const дает выражение спектральной плотности соответствующего непрерывного сигнала, умноженного на N/T0 (см. задачу 10.2):
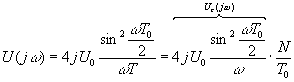 .
.
Зависимости модуля U(ω)/N от безразмерного аргумента ωT0, а также соответствующая кривая для непрерывного сигнала Uс(ω) (сплошная линия 1), изображены на рис. П19.3 для N = 8 (кривая 2) и N = 32 (штриховая кривая 3).

Рис. П19.3
Очевидно, что в последнем случае первые два лепестка спектра дискретного сигнала, пронормированного указанным способом, в диапазоне частот 0 < ωT0 < 4π практически совпадают со спектром непрерывного сигнала.
При работе в режиме изучения теоретического материала вернитесь назад к тексту Лекции 21.