26.1. УРАВНЕНИЯ ЛИНИИ В ОПЕРАТОРНОЙ ФОРМЕ
Для анализа переходных процессов вернемся к уравнениям линии в их общей форме:
Один из возможных путей решения этих уравнений — применение операторного метода. Ограничиваясь нулевыми начальными условиями, что соответствует подключению незаряженной линии к источнику, когда при t = 0 u(x, 0) = 0 и i(x, 0) = 0, перейдем к операторной форме уравнений:
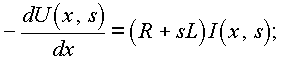
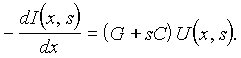
Формально ее решение ничем не отличается от решения комплексных уравнений (п.25.1), единственное различие состоит в замене оператора jw на s:
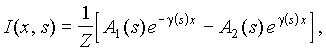
где 
—
операторный коэффициент распространения; 
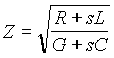— операторное волновое
сопротивление; постоянные A1 и A2 определим из условий, связывающих токи и напряжения в начале и конце линии. Например, при подаче напряжения
u0(t) от источника ЭДС с внутренним операторным сопротивлением
Z0(s) на вход линии, нагруженной на операторное сопротивление Zн(s), условия в начале и в конце линии имеют вид:
;
,
где U0(s) — операторное изображение u0(t).
Подстановка в эти условия решений для напряжения и тока U(x, s) и I(x, s) приводит их к системе, из которой определяются A1(s) и A2(s), что позволяет получить изображения для напряжения и тока, удовлетворяющие граничным условиям. Однако в данном случае изображения и не являются рациональными дробями, как при расчете цепей с сосредоточенными параметрами. Тем не менее, для нахождения их оригиналов возможно применение теоремы разложения, если они представляют однозначные функции переменной s.
