Использование кусочно-линейной аппроксимации характеристик приводит нелинейные уравнения состояния к системе линейных дифференциальных уравнений на каждом интервале изменения переменных состояния. Для интегрирования этой системы можно использовать развитый аппарат решения линейных задач. Переход к каждому следующему интервалу, отвечающему иной комбинации отрезков ломаных характеристик, приводит к изменению коэффициентов в уравнениях системы при непрерывности переменных состояния. Это используется в качестве начального условия при интегрировании на данном интервале — определение постоянных интегрирования осуществляется на базе сопряжения (припасовывания) решений для переменных состояния на соседних интервалах. Поэтому такой метод также носит название метода припасовывания или метода сопряжения интервалов. Таким образом, нелинейная задача заменяется совокупностью линейных задач, рассматриваемых последовательно по мере достижения переменными состояния значений, при которых происходит переход с одного отрезка ломаной характеристики на другой. 

Метод обладает определенной наглядностью: такая аппроксимация характеристик отвечает постоянству дифференциальных параметров нелинейных элементов на отдельных отрезках их характеристик, и решение сводится к рассмотрению последовательности задач с постоянными дифференциальными параметрами нелинейных элементов, значения которых изменяются при достижении переменной состояния определенной величины, что эквивалентно коммутациям в ветвях с нелинейными элементами. Очевидно, что рассматриваемый метод имеет общий характер и может использоваться для расчета как переходных, так и периодических процессов в нелинейных цепях. В последнем случае последовательность прохождения интервалов имеет циклический характер.

Изложим подробнее схему метода применительно к автономной цепи 1-го порядка, описываемой дифференциальным уравнением . Пусть k-ый отрезок ломаной, аппроксимирующей функцию f(x) — фазовую траекторию (рис. 29.9), выражается линейной зависимостью

,

где и , и — значения функции f(x) и искомой переменной x в начале и в конце интервала; и — приращения этих величин; .

Рис. 29.9

Подставим последнюю зависимость в уравнение состояния и запишем его в форме с разделенными переменными: . Интегрируя обе части равенства на k-м интервале, получим:

,

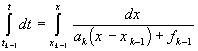или

где — время начала k-го интервала.

Для продолжительности интервала , за который переменная состояния изменится от значения до , имеем

.

Таким образом, если по значениям x_k, отвечающим границам отрезков аппроксимирующей ломаной, из уравнения состояния найдены отвечающие им значения f_k, само построение ломаной и связанные с ним вычисления можно не производить, а воспользоваться последней формулой для определения отдельных интервалов времени Dt_k, за которые проходятся отрезки ломаной. Если удовлетворительная аппроксимация нелинейной характеристики обеспечивается даже при небольшом числе отрезков, и точки t_k(x_k),отвечающие границам интервалов, дают недостаточную информацию о характере процесса, промежуточные точки t(x), лежащие внутри интервалов, можно рассчитывать, используя выражение (29.1).

Если на некотором отрезке и , т. е. значение правой части уравнения состояния сохраняется постоянным на отрезке f(x) = f_k-1 = const, то из уравнения состояния можно найти непосредственно или .

Для первого отрезка  в качестве x_k-1берется начальное значение x(0), а в качестве f_k-1  — соответствующая ему величина  f(0) (см. рис. 29.9).

Проиллюстрируем метод на примере расчета подключения цепи с последовательным соединением нелинейного резистора с характеристикой u(i) и линейной индуктивности к источнику постоянного напряжения (рис. 29.10). Цепь описывается уравнением , или в нормальной форме .

,

откуда ; ; , где . Применяя общую формулу для продолжительности прохождения k-го отрезка характеристики, получим:

,

где t_k = L Di_k/Du_k = L /R_k — постоянная времени на k-м отрезке.

Последнее выражение показывает, что в рассматриваемом случае непосредственный анализ процесса на отдельных отрезках можно опустить, так как все его параметры определяют по узловым точкам характеристики нелинейного элемента u_k и i_k.

Описанный подход можно применять и к цепям с более сложной структурой, однако здесь следует использовать непосредственно интегрирование линеаризованных уравнений на интервалах линеаризации, осуществляемое с помощью методов анализа линейных цепей (см. лекцию 17).

Пример расчета переходного процесса рассмотренным методом приведен в Задаче 25.1.

---

Дальше  (если вы еще не изучали п. 29.6)
Обратно к плану данной лекции
Дальше к плану следующей лекции