
Тема 24. ПЕРЕХОДНЫЕ ПРОЦЕССЫ В ЦЕПЯХ С РАСПРЕДЕЛЕННЫМИ ПАРАМЕТРАМИ
(задачи с решением)
Перейти к задачам без решения
При нагрузке на резистор имеем: а) отраженные волны не возникают
qu = 0, и uψ = 0 при
R = Z, б) это равенство, как и равенство варианта г), не может быть выполнено ни при каких значениях сопротивления
R, так как отраженные волны не могут по модулю превосходить
падающих волн, в) условие qu = 0,5, и
uψ = 0,5uφ выполняется при
R = 3Z; при этом получаем qi = - 0,5 и
iψ = - 0,5iφ, так что условие варианта д) также выполняется при
R = 3Z, е) условия qi = -1 и
iψ = -
iφ выполняются при
R = ¥
— для разомкнутой на конце линии. При параллельном подключении индуктивности к нагрузочному резистору эти же условия сохраняют силу для момента возникновения отраженной волны, так как в этот момент времени катушку можно считать разомкнутой. Поэтому при последовательном включении нагрузочных элементов может быть выполнено лишь условие д), причем независимо от величины сопротивления резистора.
При работе в режиме изучения теоретического материала вернитесь назад к тексту
Лекции 26.
а) При согласованной нагрузке R
= Z имеем
iψ = 0. Условия вариантов б) и в) не могут быть выполнены ни при каких значениях R. г) и е) Условия qi = -
0,5 и
iψ = - 0,5iφ и одновременно qu = 0,5, uψ = 0,5uφ
выполняются при R = 3Z. д) Условия
qu = -1 и uψ = - uφ выполняются при
R = 0 — для короткозамкнутой на конце линии. В момент возникновения отраженной волны незаряженный конденсатор можно рассматривать как короткозамкнутый элемент цепи, и его присутствие в схеме никак не влияет на характер отраженных волн.
При работе в режиме изучения теоретического материала вернитесь назад к тексту
Лекции 26.
|
Задача 24.3. На вход линии без потерь длиной
l = 10 км с волновым сопротивлением
Z = 75 Ом подается импульс напряжения от генератора через четырехполюсник (рис.
П24.1). Рассчитать и построить распределение напряжения и тока вдоль линии для момента времени, когда отраженная от нагрузки волна достигнет середины линии. Скорость распространения волны равна
v = 2 ×
105 км/с.

Рис. П24.1
|
Связь напряжения и тока прямой волны
uφ и iφ: uφ = iφZ показывает, что влияние линии на формирование прямой волны может быть учтено введением в расчетную схему, состоящую из источника
U0 и входного четырехполюсника, резистора с сопротивлением, равным волновому, подключенного к выходу четырехполюсника (рис. П24.2).
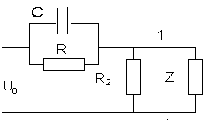
Рис. П24.2
В эту схему не включаются элементы нагрузки на конце линии, так как характеристики прямой волны не зависят от нагрузки.
Расчет переходного процесса в схеме замещения при нулевых начальных условиях выполняется любым известным методом расчета переходных процессов в цепях с сосредоточенными параметрами. Так, при использовании операторного метода найдем входное сопротивление
 ,
,
где R2' = R2Z/(R2 + Z).
Тогда операторное изображение напряжения в начале линии — напряжения прямой волны
Uφ(s) равно
 .
.
Подстановка числовых значений приводит к результатам:
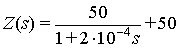 ;
;
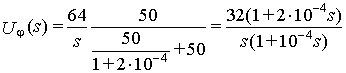 .
.
Применяя теорему разложения, найдем параметры волны в начале линии:
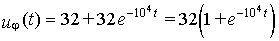 (В).
(В).
Для тока прямой волны получим:
 (А).
(А).
Напряжение отраженной от нагрузки волны
uψ определим с помощью операторного коэффициента отражения:
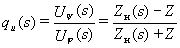 ,
,
где Zн(s) — операторное входное сопротивление нагрузки. Для изображенной на рис. П24.1 схемы нагрузки имеем:
 .
.
Изображение напряжения отраженной волны примет вид:
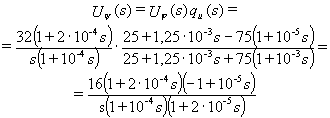
При записи оригинала uψ учтем, что отраженная волна возникает в момент времени прихода прямой волны к нагрузке, и поэтому начало отсчета времени
t' для отраженной волны запаздывает относительно подачи напряжения на вход линии на время пробега прямой волны вдоль линии
l/v: t' = t – l/v. Применение теоремы разложения дает для напряжения отраженной волны на нагрузке:
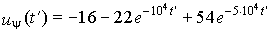 (В).
(В).
Так как ток обратной волны 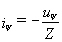 , то
, то
 (А).
(А).
При записи выражений, описывающих волны напряжения и тока в произвольной точке линии, учтем, что вследствие конечной скорости распространения волн изменения тока и напряжения волны приходят точку с координатой
x с задержкой, равной времени пробега волны до этой точки
x/v. Поэтому для прямой волны в полученных выражениях
uφ и iφ, соответствующих началу линии (x = 0), следует заменить аргумент
t на 
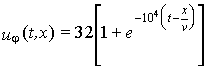 ,
,
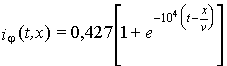 .
.
Рассчитанные выше выражения напряжения и тока обратной волны относятся к концу линии (x = l). Отсчитывая расстояние
x' от конца линии к началу (x' = l - x), аналогично запишем для произвольной точки линии, заменяя аргумент
t' на 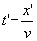 :
:
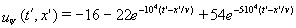 (В).
(В).
Так как ток обратной волны 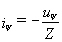 , то
, то
 (А).
(А).
Результирующие величины определяются суммированием напряжений и токов в тех точках, где к рассматриваемому моменту времени имеются обе волны:
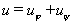 ,
,
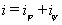 .
.
Отсюда следует, что хотя графики, выражающие напряжение и ток отдельных волн подобны друг другу, результирующие ток и напряжение имеют различный вид.
Распределение напряжения и тока для рассматриваемого момента времени, рассчитанное по полученным формулам, приведено на рис. П24.3.
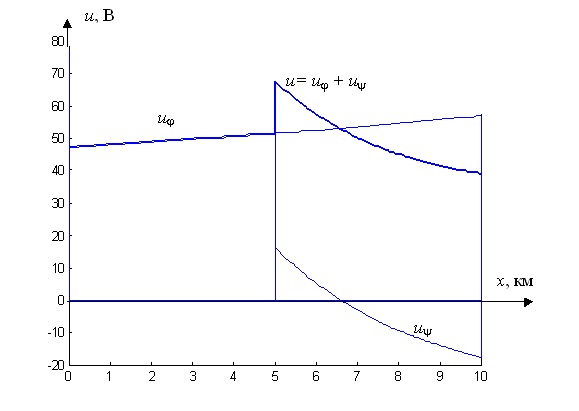
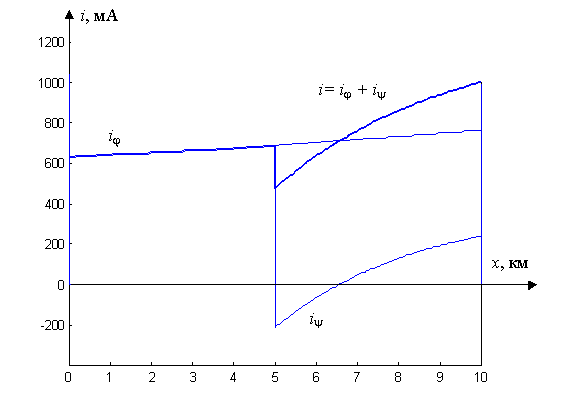
Рис. П24.3
При работе в режиме изучения теоретического материала вернитесь назад к тексту
Лекции 26.
Конец
Обратно к списку тем практических занятий
Обратно к плану соответствующей лекции
![]() , б)
, б) ![]() , в)
, в) ![]() , г)
, г) ![]() , д)
, д) ![]() , е)
, е) ![]() . Изменится ли ответ для отраженных волн в момент их возникновения, если параллельно или последовательно с нагрузочным резистором включена индуктивность?
. Изменится ли ответ для отраженных волн в момент их возникновения, если параллельно или последовательно с нагрузочным резистором включена индуктивность?

 ,
,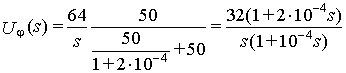 .
.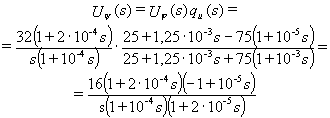
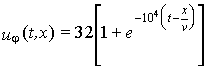 ,
,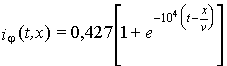 .
.
