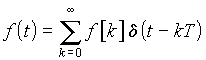21.1. ДИСКРЕТНОЕ ПРЕОБРАЗОВАНИЕ ЛАПЛАСА, Z-ПРЕОБРАЗОВАНИЕ, ЕГО ОСНОВНЫЕ СВОЙСТВА

При расчете переходных процессов, связанных с действием в цепи непрерывных сигналов, мы использовали либо метод переменных состояния, в основе которого лежит интегрирование дифференциальных уравнений, либо операторный метод, сводящий операции между напряжениями и токами элементов цепи к алгебраическим соотношениям для их изображений. При анализе действия дискретных сигналов первому из них отвечает рассмотренное выше решение разностных уравнений. Остановимся теперь на втором методе анализа импульсных систем, использующем, как и операторный метод, переход от операций над самими сигналами во временной области к действиям над их изображениями в частотной области. Он сводит разностные соотношения между сигналами дискретного времени — решетчатыми функциями — к алгебраическим связям между их изображениями.

Применим обычное преобразование Лапласа к соотношению непрерывного времени

,

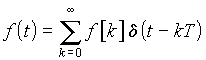выражающему последовательность d-импульсов (см. рис. 20.6, б). Так как изображение по Лапласу функции d (t – kТ) равно e^–skТ, то для рассматриваемой последовательности имеем

.

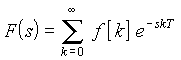Последовательность прямоугольных импульсов (см. рис. 20.6, а)

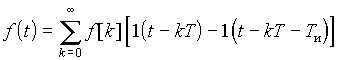
имеет изображение:

.

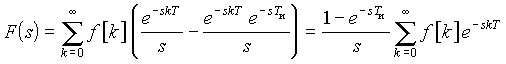Нетрудно показать, что операторное изображение F(s) любой последовательности импульсов одинаковой формы будет иметь аналогичную структуру – оно приводится к сумме 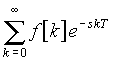, а форма импульсов определяет дополнительный множитель перед суммой.

Поэтому дискретное преобразование Лапласа произвольной решетчатой функции f[k] определяется соотношением

.

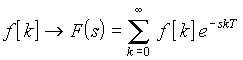Оператор e^–sT в этой формуле имеет смысл оператора запаздывания на время одного шага Т. При определении воздействия дискретного сигнала на цепь этот экспоненциальный множитель будет входить во все соотношения. Поэтому обозначая e^sT сокращенно символом z, мы приходим к z-преобразованию, для которого формула прямого преобразования имеет вид

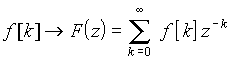
Поскольку z-преобразование выражает главную часть ряда Лорана, оно также называется преобразованием Лорана. Условия сходимости z-преобразования связаны со сходимостью исходного преобразования Лапласа. Напомним, что для сходимости интеграла Лапласа 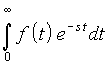вещественная часть переменной s = s + jw должна обеспечить при s > s₀ сходимость интеграла даже при растущей функции f(t). Так как комплексные переменные s и z связаны соотношением z = e^sT = e^sT e^jwT, то модуль ½  z ½  = e^sT выбирается таким, чтобы ряд F(z) сходился и для возрастающей последовательности f[k]. Таким образом, F(z) сходится вне круга с радиусом . Из сказанного следует, что z-преобразование существует для последовательностей f[k], растущих при k ®  ¥ не быстрее экспоненциальной последовательности e^s0^kT.

z-изображение решетчатых функций, изображение разностей. Так же, как и при изучении свойств преобразования Лапласа, когда мы в качестве "ключевой" функции рассматривали экспоненту, определим z-преобразование экспоненциальной решетчатой функции f[k] = e^ak. Согласно общей формуле имеем 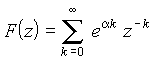. При выполнении условия сходимости — выбора модуля ½ z ½ > e^a — это бесконечная убывающая геометрическая прогрессия. Применяя известную формулу для ее суммы, получим

.

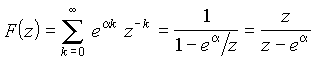Следует обратить внимание на сходство полученного результата с преобразованием Лапласа экспоненциальной функции e^at ® 1/(s - a). Заметим, что множитель a в показателе решетчатой экспоненты может быть и комплексным. Это позволяет, в частности, получить z-изображения решетчатых функций, изменяющихся, например, по закону синуса, выражая их через экспоненты с помощью формулы Эйлера. Из полученного изображения вытекает также представление решетчатой функции, принимающей постоянное значение  f[k] = f₀. Полагая в полученной формуле a = 0 и умножая на постоянную f₀, найдем 

.

Изображения некоторых решетчатых функций и другие соотношения z-преобразования приведены в Приложении 5. Примеры z-преобразования решетчатых функций приведены в Задаче 19.1.

Многие свойства z-преобразования в определенном смысле аналогичны свойствам  преобразования Лапласа. Сюда относится, в частности, изображение смещенной последовательности, являющееся аналогом теоремы запаздывания.  Пусть последовательность f[k] имеет изображение F(z). Найдем z-изображение F₁(z) такой же последовательности, смещенной на один шаг f[k + 1]:

.

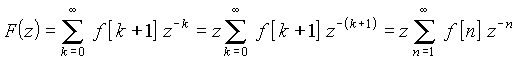В последнем равенстве мы произвели замену k + 1 = n. Добавление и вычитание из последнего результата величины zf[0] позволяет выделить в нем z-изображение исходной последовательности

.

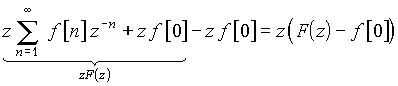Таким образом, окончательно

.

Изображение разности Df[n] = f[n + 1] – f[n] получим, вычитая изображения f[n + 1] и f[n]:

.

Для вывода формулы обратного z-преобразования — нахождения последовательности f[k] по ее изображению F(z) — используем выражение для коэффициентов ряда Лорана. Поскольку результат прямого преобразования представляет собой ряд Лорана в окрестности бесконечно удаленной точки, то для вычисления коэффициентов этого ряда имеем формулу

,

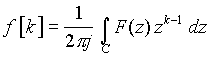где интегрирование производится по контуру с, охватывающему все особые точки функции F(z), например, окружность (рис. 21.1).

Однако, как и в преобразовании Лапласа, применение общей формулы обратного z-преобразования чаще заменяется более простыми выкладками. Если подынтегральная функция F(z) имеет особенности только в виде полюсов, то контурный интеграл на комплексной плоскости можно вычислить с помощью теоремы о вычетах

,

где суммирование ведется по всем полюсам функции.

Если изображение представляет рациональную дробь F(z) = G(z)/H(z), а F(z)z^k–1 имеет только простые полюса, отличные от нуля, применение правила вычисления вычетов в простых полюсах позволяет получить формулу

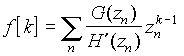
где z_n – корни знаменателя F(z), т. е. уравнения H(z) = 0, а H'(z) = dH/dz. Легко увидеть, что и эта формула является аналогом теоремы разложения для преобразования Лапласа.

Однако, при обратном z–преобразовании изображения с кратными полюсами встречаются чаще чем при обычном   преобразовании Лапласа. Например, к кратным полюсам приводят решетчатые функции, описывающие конечные последовательности, а также последовательности с нулевыми начальными членами. В этом случае для определения оригинала f[k] используют формулу вычисления вычетов в кратных полюсах. Можно также применить  разложение F(z) в ряд по отрицательным степеням z^–k, приводящее изображение к виду ряда прямого z–преобразования, k–й член которого выражает значение  f[k].

---

Дальше
Обратно к плану лекции