20.4. РАЗНОСТНЫЕ УРАВНЕНИЯ ПРОСТЕЙШИХ ЦЕПЕЙ, ИХ НЕПОСРЕДСТВЕННОЕ РЕШЕНИЕ

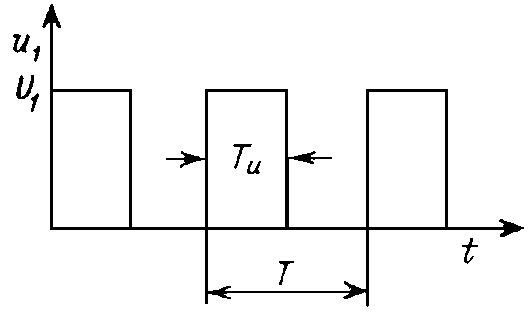
Пусть на входе интегрирующей цепи (см. рис. 20.1, а,б) действует последовательность прямоугольных импульсов с амплитудой U₁, длительностью T_и, следующих с интервалом T (рис. 20.9).

Рис. 20.9

Рассмотрим процессы в цепи на n-м интервале nT < t < (n + 1)T. В начале напряжение u₂ нарастает по закону u₂(t') = U₁ + (– U₁ + u₂[n]) e^–t'/t, где t' = t – nT.

К моменту t' = T_и оно достигает значения u₂(T_и) = U₁ + (u₂[n] – U₁) e^–T_и/t. В промежутке T_и < t' < T входное напряжение равно нулю, а выходное напряжение спадает по экспоненте: u₂(t') = u₂(T_и) e^{–(t'– Tи)/t}. В результате к моменту появления на входе цепи следующего импульса (t' = T) напряжение u₂ становится равным

.

Группируя члены, окончательно получим

.

(20.1)

Это соотношение представляет собой линейное неоднородное разностное уравнение 1-го порядка. Теория решения таких уравнений аналогична теории дифференциальных уравнений. Решение имеет две составляющие

,

представляющие частное решение неоднородного уравнения и общее решение соответствующего однородного уравнения . Последнее будем искать в виде . Подставляя эту форму в однородное уравнение, найдем q = e^–T/t, поэтому общее решение неоднородного разностного уравнения можно записать в виде u₂[n] = A₁qⁿ + A₂. Обе постоянные определяют из условий при t = 0 и t ®  ¥. Так как при t = 0 (n = 0) выходное напряжение u₂ = u_C отсутствует, u₂[0] = 0. Учитывая, что в цепи при t ®  ¥ устанавливается стационарный режим, при n ®  ¥ имеем u₂[n + 1] ® u₂[n].

Оба эти условия позволяют определить значения постоянных A₁ и A₂ из системы:

;

,

откуда

.

.

В случае, когда действующие на входе цепи прямоугольные импульсы имеют переменную амплитуду, описываемую решетчатой функцией u₁[n], в разностном уравнении (20.1) следует заменить U₁ на u₁[n]. В результате уравнение принимает вид

,

где a = e^– T/t, .

Получим разностное уравнение для произвольной цепи 1-го порядка, находящейся под действием последовательности прямоугольных импульсов длительностью T_и и амплитудами u₁[n]. Будем рассматривать лишь цепи с ограниченной импульсной характеристикой, для которых h(0) = 0 и h_d имеет всюду конечное значение.

Если на n-ом интервале действующий на входе импульс u₁[n] отсутствует, то в цепи 1-го порядка все токи и напряжения изменяются по экспоненциальному закону e^–t/t, где t — постоянная времени цепи. Поэтому за время T выходная величина изменится от значения u₂[n] до значения . Если же предположить, что в начале интервала u₂[n] = 0, то выходное напряжение к концу интервала определится только действием входного импульса. Эту составляющую с помощью переходной характеристики h(t) можно определить как разность:

,

рассматривая импульс длительностью T_и как включаемое в начале интервала напряжение u₁[n] и включаемое при t = T_и отрицательное напряжение такой же величины – u₁[n]. Применяя принцип наложения, получим искомое разностное уравнение для цепи 1-го порядка при действии прямоугольных импульсов

.

Переходя к пределу при T_и ®  0, получим уравнение, описывающее поведение цепи при действии d-импульсов. При T_и ®  0 h(T) – h(T – T_и) ®  h_d(T) T_и. В результате разностное уравнение приводится к виду

,

где  — площадь d-импульса. Полученное уравнение выражает напряжение на выходе цепи до начала действия очередного d-импульса u₁^*[n + 1]. После подачи этого импульса выходное напряжение изменяется скачком на величину Du₂[n + 1] = u₁[n + 1]h_d(+ 0).

Пример составления разностного уравнения для цепи 1-го порядка рассмотрен в Задаче 18.1.

---

Дальше
Обратно к плану лекции