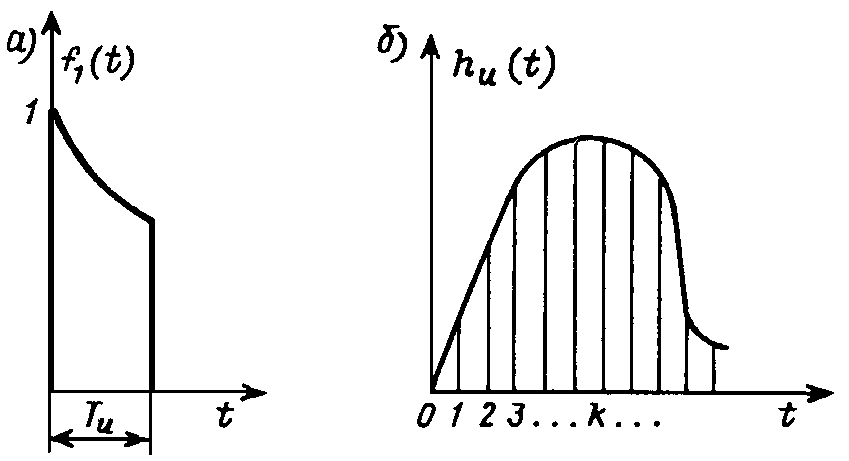
20.6. ДИСКРЕТНАЯ РЕАКЦИЯ ЦЕПИ НА ДЕЙСТВИЕ ОДИНОЧНОГО ИМПУЛЬСА. ДИСКРЕТНАЯ ИМПУЛЬСНАЯ ХАРАКТЕРИСТИКА. ДИСКРЕТНАЯ СВЕРТКА
Реакция цепи на действие единичного d-импульса описывается импульсной характеристикой hd(t). Аналогично можно описать реакцию цепи на действие одиночного импульса произвольной формы, подаваемого на вход цепи в момент времени t = 0. Такой импульс с единичной интенсивностью — амплитудой (рис. 20.10, а) или площадью — создаст на выходе рассматриваемой цепи некоторый сигнал (рис. 20.10, б).
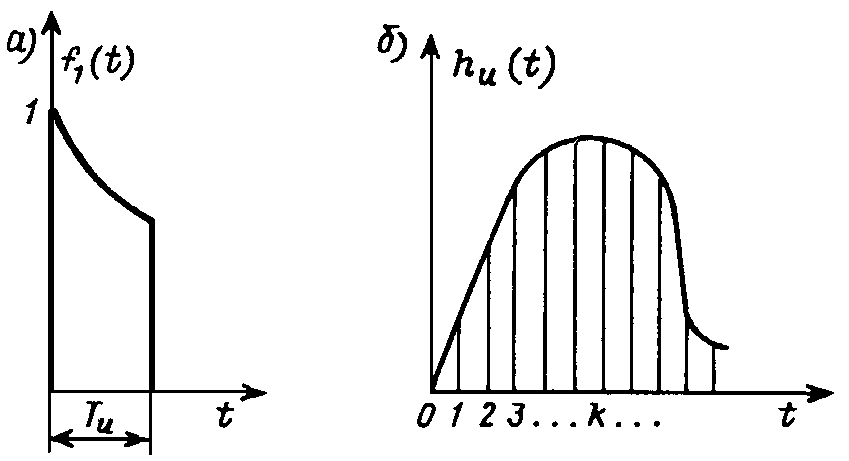
Рис. 20.10
Подобная характеристика — реакция цепи на одиночный импульс с единичной интенсивностью hи(t) — позволяет рассчитать поведение цепи при действии на входе последовательности импульсов, имеющих одинаковую форму.
Дискретная импульсная характеристика hи[k] — это решетчатая функция, отвечающая сигналу hи(t). Она представляет его выборку в моменты времени kT (T > Tи):
![]() .
.
Рассмотрим далее цепь, находящуюся под действием последовательности импульсов сложной формы, следующих друг за другом с шагом T, интенсивность которых описывается решетчатой функцией f1[k] (рис. 20.7). Реакция цепи на такую последовательность представляется суммой реакций на каждый импульс с учетом времени задержки
![]() .
.
Это соотношение и представляет дискретную свертку.
Если на входе цепи действует последовательность d-импульсов, площади которых описываются функцией f1*[k], последнее выражение можно записать в виде
![]() ,
,
где hd[k] = hd(kT) – выборка импульсной характеристики цепи.
Определим дискретные характеристики цепей при действии на входе прямоугольных импульсов длительностью
Tи с единичной амплитудой. Реакцию цепи на одиночный такой сигнал можно определить как реакцию цепи на единичную функцию
1(t) и отрицательную единичную функцию, задержанную на время
Tи:
![]() ,
,
а дискретная импульсная характеристика для k = 1, 2, ... имеет вид
![]() .
.
При k = 0 hи[0] = h(0) = 0. Так, для простейших интегрирующих цепей (рис. 20.1, а, б) имеем
![]() и
и
![]()
Рассмотрим реакцию такой цепи на последовательности прямоугольных импульсов со знакопеременной амплитудой u1[k] = U0(– 1)k (рис. 20.11).
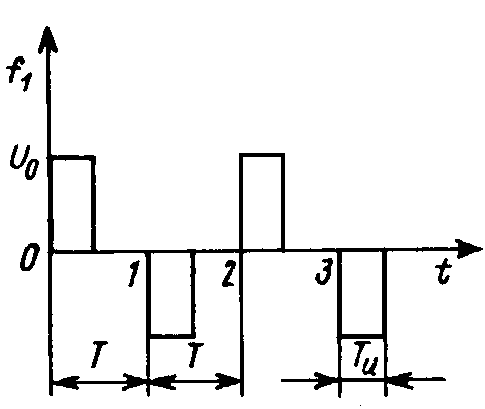
Рис. 20.11
В этом случае выражение дискретной свертки дает:

Верхний предел суммирования взят в соответствии с тем, что hи[0] = 0. Применяя формулу суммирования геометрической прогрессии, окончательно получим
![]() .
.
Нетрудно убедиться в том, что использование дискретной свертки в ранее рассмотренном примере о расчете реакции цепи на последовательность импульсов с одинаковой амплитудой U0 (рис. 20.9) дает тот же результат, что и непосредственное решение разностного уравнения. Однако применение дискретной свертки представляет более общий путь решения.