Тема 5. МЕТОД СИГНАЛЬНЫХ ГРАФОВ (задачи с решением)
Перейти к задачам без решения
|
Задача 5.1. Построить сигнальный граф на основе метода узловых напряжений (см. п. 5.3) и определить с его помощью напряжение на резисторе R3 в схеме рис. П4.2, а, рассмотренной в Задаче 4.2. |
Рис. П5.1
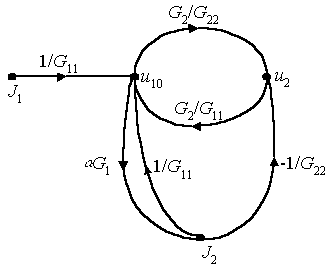
Выделим на графе рис. П5.1 узлы, соответствующие источникам тока J1 и J2, а также узловым напряжениям u10 и u20. Узлы u10 и u20 соединим ветвями G2G11 и G2/G22 (где G11 = G1 +G2, G22 = G2 +G3 — собственные проводимости узлов), отвечающими их общей ветви с проводимостью G2. Далее изобразим ветвь, соединяющую узлы J1 и u10, с передачей 1/G11 и две ветви, соединяющие узел J2 с узлами u10 и u20. Их передачи равны, соответственно1/G11 и - 1/G22. Поскольку ток управляемого источника тока J2 выражается через узловое напряжение u10 как J2 = αi1 = αG1u10, то этому соотношению отвечает ветвь графа, соединяющая узел u20 с узлом J2. Ее изображение завершает построение сигнального графа.
При работе в режиме изучения теоретического материала вы можете вернуться назад к тексту n. 5.4.
Для определения выходного напряжения
u20 с помощью формулы Мейсона (см. п. 5.6), найдем пути, соединяющие узел
J1
— исток графа — с выходным узлом u20. Таковыми являются путь J1u10u20 с передачей
J1u10J2u20 с передачей
. Построенный граф имеет три контура u10u20u10, u10J2u10 и
u10J2u20u10. Их передачи равны, соответственно,
, 
и 
. Поскольку все контуры имеют общий узел
u10, несоприкасающихся среди них нет. То же относится и к путям. Поэтому передача от
J1 к u20 выражается с помощью формулы Мейсона следующим образом:
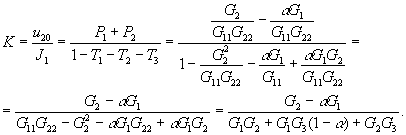
Использование значений параметров эквивалентного источника, полученных в Задаче 4.2 и подстановка численных значений, приводит, как нетрудно проверить, к тождественному результату.
