Тема 6. АНАЛИЗ ПРОСТЕЙШИХ ЦЕПЕЙ СИНУСОИДАЛЬНОГО ТОКА.
ВЕКТОРНЫЕ ДИАГРАММЫ (задачи с решением)
Перейти к задачам без решения
|
Задача 6.1. Записать выражение для мгновенного значения синусоидального тока (см. п. 7.1) с периодом T = 12 мс и действующим значением I = 2 мА, если при t = 0 мгновенный ток равен 1 мА, а через 2,31 мс ток достигнет ближайшего максимума. Является ли полученное решение единственным? |
Параметры, входящие в общее выражение для мгновенного значения тока i = Imsin(wt + y) — амплитуда Im, частота w и начальная фаза y определяются через заданные величины следующим образом
, 
.
В результате получим i = 2,828sin(523,6t + 0,3614). Многозначность функции arcsin не делает ответ многозначным, так как из условия следует, что начальная фаза находится в первой четверти.
При работе в режиме изучения теоретического материала вернитесь назад к тексту Лекции 7.
|
Задача 6.2. Построив векторную диаграмму, определить действующие значения входного напряжения и тока для цепи, схема которой изображена на рис. П6.1 при числовых данных: U1 = U3 = 20 В, U5 = 10 В, I2 = 1 А, I4 = I5 = 2 А;
Рис.П6.1 |
Построение векторной диаграммы следует начать с изображения вектора напряжения или тока, относительно которого можно однозначно сориентировать наибольшее количество векторов, отвечающих другим токам или напряжения в данной цепи.
Правила изображения на векторной диаграмме токов и напряжений на отдельных элементах цепи см. в > Табл. 7.1.
Для цепи, изображенной на рис. П6.1, такой величиной является напряжение U5, относительно которого известен фазовый сдвиг токов I5 и I4. Отложим U5 на диаграмме (рис. П6.2) вертикально. Вектор тока в резистивной ветви I5 совпадает по направлению с U5, а I4 в индуктивности отстает от U5 на угол p/2. Далее используем первый закон Кирхгофа в векторной форме и строим вектор I3 = I4 + I5.
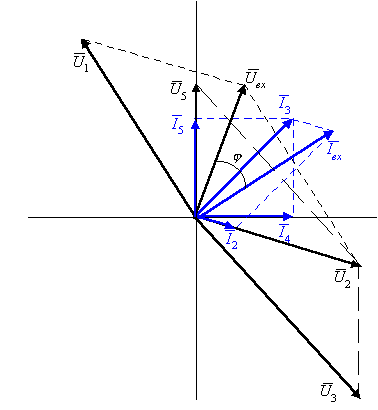
Рис. П6.2
Как следует из диаграммы: I3 = 2Ц2 А. Вектор напряжения на конденсаторе U3 отстает от I3 на p/2. Используя второй закон Кирхгофа, строим U2 = U3 + U5. Из диаграммы найдем U2 = 14 В. Ток I2 в резистивной ветви совпадает по фазе с U2. Далее суммируем векторы Iвх = I2 + I3. Численное значение этого тока определим из диаграммы: Iвх= 3,4 А. Вектор напряжения на катушке U1опережает Iвх на p/2. Наконец, строим вектор Uвх = U1 + U2 и находим Uвх = 14,8 В. Полностью векторная диаграмма изображена на рис. П6.2. Как следует из диаграммы, цепь в целом имеет индуктивный характер, так как Uвх опережает Iвх по фазе.
При работе в режиме изучения теоретического материала вернитесь назад к тексту Лекции 7.
|
Задача 6.3. Определить эквивалентные параметры
Rэ, Xэ, zэ, yэ, Bэ, Gэ двухполюсника (см. п. 7.4 теоретического материала), изображенного на рис. П6.3,
а, при
Рис. П6.3 |
помощью соотношений между эквивалентными параметрами R, X и G, B двухполюсника (п.7.4) преобразуем в исходной задаче параллельную R2C цепочку с проводимостями параллельных ветвей G2 = 1/R2 и B3 = – ωC к эквивалентной последовательной RC цепи, параметры которой определятся формулами
В результате приходим к эквивалентной цепи, изображенной на рис П6.3,
б, для которой 
. Используя вышеуказанные соотношения, найдем
по формулам yэ = 1/zэ = 0,6325 См,
При работе в режиме изучения теоретического материала вернитесь назад к тексту Лекции 7.
= 1 Ом.