Так как уравнения состояния нелинейной цепи представляют систему нелинейных дифференциальных уравнений, то в подавляющем большинстве случаев единственным средством получения решения является численное интегрирование системы, осуществляемое с помощью известных методов: Эйлера, трапеций, Рунге-Кутта и др. Техника их применения к интегрированию нелинейных систем не имеет каких-либо особенностей по сравнению с линейными системами (см. п. 18.1). 

Пример такого решения приведен в Задаче 25.1.

Поэтому проанализируем те, сравнительно редкие случаи, когда нелинейные уравнения состояния можно проинтегрировать аналитически. Не будем рассматривать те ситуации, в которых относительно малые изменения токов и напряжений, связанных нелинейными зависимостями, позволяют осуществить линеаризацию дифференциальных уравнений, как, например, при анализе малосигнального режима электронных цепей, сводящемся к решению линейной системы. 

Аналитическое решение нелинейных уравнений возможно для цепей с одним динамическим элементом (емкостью или индуктивностью), описываемых уравнением состояния 1-го порядка dx/dt = f(x, t), где x — переменная состояния. Для автономной цепи, находящейся под действием постоянных источников ЭДС и тока (или при отсутствии таковых — при замыкании зажимов цепи, обладающей запасом энергии), правая часть уравнения f не зависит от времени:

.

Это уравнение относится к классу уравнений с разделяющимися переменными и допускает решение путем неявного представления переменной состояния

,

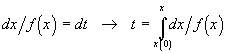где x(0) — начальное значение переменной состояния.

Для многих классов функций f(x) этот интеграл имеет аналитическое выражение. В частности, он вычисляется для рациональной функции f(x) (такой вид правая часть уравнения состояния будет иметь при аппроксимации характеристик нелинейных элементов посредством многочленов). В цепях простой структуры, например, простейших двухэлементных RC-  и RL-цепях, возможности аналитических аппроксимаций еще шире и включают и другие классы аппроксимаций характеристик, в частности, степенные и целый ряд трансцендентных функций. Это следует учитывать в случаях, когда мы сами производим аппроксимацию характеристик нелинейных элементов и свободны в выборе классов аппроксимирующих функций. 

Таким образом, возможность получения аналитических решений уравнений состояния в нелинейных цепях существует для цепей с одним динамическим элементом, находящимся под действием либо постоянных источников, либо в режиме замыкания зажимов цепи накоротко. В более сложных случаях получить такое решение за счет тех или иных замен переменных или подстановок оказывается в большинстве случаев невозможным. 

Рассмотрим в качестве первого примера переходный процесс при подключении RC-цепи с нелинейным резистором к источнику постоянного напряжения (рис. 29.7).

Значение a = 1 соответствует линейной цепи, для которой решение хорошо известно (см. п. 15.2).

Полученный результат позволяет выразить и явное представление u_C(t)  и других переменных в цепи; при нулевых начальных условиях (u_C(0) = 0) после несложных преобразований имеем:

,

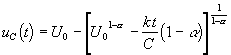а для тока в цепи

.

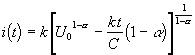Использованный вид степенной аппроксимации характеристики нелинейного элемента позволяет получить аналитические решения также и при нелинейности конденсатора в  RC-цепи с линейным резистором.

В качестве следующего примера проанализируем подключение RL-цепи с нелинейной катушкой к источнику постоянного напряжения. Процесс описывается уравнением , откуда имеем 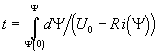. Принимая нулевое начальное условие и используя параболическую аппроксимацию катушки , приходим к табличному интегралу:

.

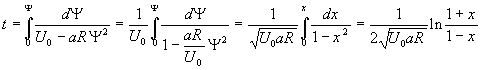где — безразмерная переменная, которую легко найти из последнего выражения:

,

где .

Переходя к размерным переменным, получим:

; .

Интересно сопоставить полученное решение с изменением тока переходного процесса при включении линейной RL-цепи к источнику постоянного напряжения (см. п. 15.3) i = U₀(1 - e^-Rt/L)/R (кривая L = const на рис. 29.8). В нелинейной цепи дифференциальная индуктивность в начале процесса значительно превышает индуктивность в установившемся режиме, когда потокосцепление достигает максимального значения . Поэтому в начале процесса нарастание тока в нелинейной цепи существенно замедлено (кривая на рис. 29.8). 

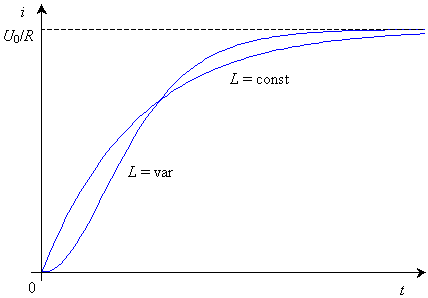
Рис. 29.8

По мере насыщения индуктивность катушки падает, что ведет к убыстрению нарастания тока по сравнению с линейной цепью (кривая L = const).